Near-IR Ruled Reflective Diffraction Gratings
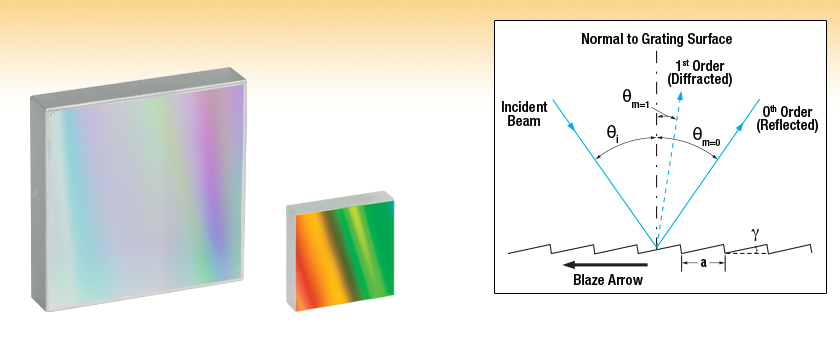
- Gratings with 750 nm to 1600 nm Blaze Wavelengths
- High Grating Efficiency of 60 to 80% at the Blaze Wavelength
GR50A-0610
50 mm x 50 mm
1 µm Blaze
Wavelength
GR25-0608
25 mm x 25 mm
750 nm Blaze
Wavelength
See the Gratings Tutorial Tab Below for Definitions and Equations

Please Wait
| Selection Guide | |
|---|---|
| Transmission Gratings | |
| Ruled | UV |
| Visible | |
| Near IR | |
| Volume Phase Holographic |
Visible |
| Near IR | |
| Reflective Gratings | |
| Ruled | UV |
| Visible | |
| Near IR | |
| Mid IR | |
| Holographic | |
| Echelle | |

Click to Enlarge
Diffraction Grating Mounted in
Polaris Mirror Mount Using Diffraction Grating Adapter
Features
- Blaze Wavelengths from 750 to 1600 nm
- High Grating Efficiency of 60 to 80% at the Blaze Wavelength
- Low Ghosting, <0.5% of Parent Line
- Aluminum Reflective Coating
- Soda Lime Glass Substrate with 300 to 1200 Grooves/mm
- Produced from Ruled Original
Thorlabs offers ruled diffraction gratings for use in the near-IR region. These gratings will have a relatively sharp efficiency peak about their blaze wavelength and are produced from ruled originals. They are offered with different blaze angles to suit a variety of applications in spectroscopy and analysis where high efficiency is of primary concern. For more information, please click on the Gratings Tutorial tab above. We also offer reflective holographic gratings, which do not produce ghosting effects at the expense of efficiency. For information regarding the differences between grating types, please click on the Gratings Guide tab above.
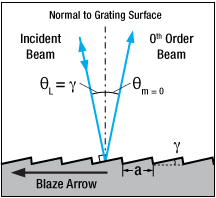
Click to Enlarge
Ruled Diffraction Grating Used in
Littrow Configuration (θi=γ)
(Note: 1st Order Beam is Collinear and Antiparallel to Incident Beam)
Please note that these gratings are bare aluminum and do not contain an overcoat. However, custom MgF2 or gold coatings are available to protect the aluminum surface of the gratings. The gold coating offers high performance in the IR, while the MgF2 coating offers the best protection; contact Tech Support for further details.
Mounts and Adapters
Thorlabs offers a variety of mounts and adapters for precise and stable mounting and aligning square optics. All of Thorlabs' gratings can be mounted directly into the KM100C Right-Handed or KM100CL Left-Handed Kinematic Rectangular Optic Mount. Gratings can also be mounted in one of three Kinematic Grating Mount Adapters which can be used with any of Thorlabs' Ø1" Mirror Mounts, including the POLARIS-K1E Ultra-Stable Kinematic Mirror Mount.
Warning
Optical gratings can be easily damaged by moisture, fingerprints, aerosols, or the slightest contact with any abrasive material. Gratings should only be handled when necessary and always held by the sides. Latex gloves or a similar protective covering should be worn to prevent oil from fingers from reaching the grating surface. No attempt should be made to clean a grating other than blowing off dust with clean, dry air or nitrogen. Solvents will likely damage the grating's surface.
Thorlabs uses a clean room facility for assembly of gratings into mechanical setups. If your application requires integrating the grating into a sub-assembly or a setup please contact Tech Support to learn more about our assembly capabilities.
Diffraction Gratings Tutorial
- Introduction
- Blazed (Ruled) Gratings
- Volume Phase Holographic Transmission Gratings
- Holographic Reflective Gratings
Introduction
Diffraction gratings, either transmissive or reflective, can separate different wavelengths of light using a repetitive structure embedded within the grating. The structure affects the amplitude and/or phase of the incident wave, causing interference in the output wave. In the transmissive case, the repetitive structure can be thought of as many tightly spaced, thin slits. Solving for the irradiance as a function wavelength and position of this multi-slit situation, we get a general expression that can be applied to all diffractive gratings when = 0°,
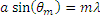
(1)
known as the grating equation. The equation states that a diffraction grating with spacing will deflect light at discrete angles (
), dependent upon the value
λ, where
is the order of principal maxima. The diffracted angle,
, is the output angle as measured from the surface normal of the diffraction grating. It is easily observed from Eq. 1 that for a given order
, different wavelengths of light will exit the grating at different angles. For white light sources, this corresponds to a continuous, angle-dependent spectrum.
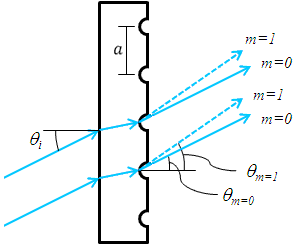
Figure 1. Transmission Grating
Transmission Gratings
One popular style of grating is the transmission grating. The sample diffraction grating with surfaces grooves shown in Figure 1 is created by scratching or etching a transparent substrate with a repetitive series of narrow-width grooves separated by distance . This creates areas where light can scatter.
The incident light impinges on the grating at an angle , as measured from the surface normal. The light of order
exiting the grating leaves at an angle of
, relative to the surface normal. Utilizing some geometric conversions and the general grating expression (Eq. 1) an expression for the transmissive diffraction grating can be found:
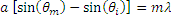
(2)
where both and
are positive if the incident and diffracted beams are on opposite sides of the grating surface normal, as illustrated in the example in Figure 1. If they are on the same side of the grating normal,
must then be considered negative.
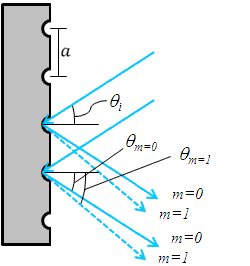
Figure 2. Reflective Grating
Reflective Gratings
Another very common diffractive optic is the reflective grating. A reflective grating is traditionally made by depositing a metallic coating on an optic and ruling parallel grooves in the surface. Reflective gratings can also be made of epoxy and/or plastic imprints from a master copy. In all cases, light is reflected off of the ruled surface at different angles corresponding to different orders and wavelengths. An example of a reflective grating is shown in Figure 2. Using a similar geometric setup as above, the grating equation for reflective gratings can be found:
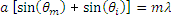
(3)
where is positive and
is negative if the incident and diffracted beams are on opposite sides of the grating surface normal, as illustrated in the example in Figure 2. If the beams are on the same side of the grating normal, then both angles are considered positive.
Both the reflective and transmission gratings suffer from the fact that the zeroth order mode contains no diffraction pattern and appears as a surface reflection or transmission, respectively. Solving Eq. 2 for this condition, =
, we find the only solution to be
=0, independent of wavelength or diffraction grating spacing. At this condition, no wavelength-dependent information can be obtained, and all the light is lost to surface reflection or transmission.
This issue can be resolved by creating a repeating surface pattern, which produces a different surface reflection geometry. Diffraction gratings of this type are commonly referred to as blazed (or ruled) gratings. More information about this can be found in the section below.
Blazed (Ruled) Gratings
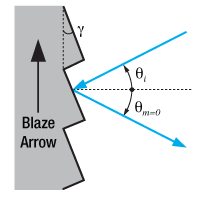
Figure 4. Blazed Grating, 0th Order Reflection
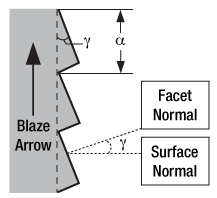
Figure 3. Blazed Grating Geometry
The blazed grating, also known as the echelette grating, is a specific form of reflective or transmission diffraction grating designed to produce the maximum grating efficiency in a specific diffraction order. This means that the majority of the optical power will be in the designed diffraction order while minimizing power lost to other orders (particularly the zeroth). Due to this design, a blazed grating operates at a specific wavelength, known as the blaze wavelength.
The blaze wavelength is one of the three main characteristics of the blazed grating. The other two, shown in Figure 3, are , the groove or facet spacing, and
, the blaze angle. The blaze angle
is the angle between the surface structure and the surface parallel. It is also the angle between the surface normal and the facet normal. Note that Figure 3 also defines the direction of the "blaze arrow"; this arrow is visibly marked on one edge of all Thorlabs' blazed transmission gratings.
The blazed grating features geometries similar to the transmission and reflection gratings discussed thus far; the incident angle () and
th order reflection angles (
) are determined from the surface normal of the grating. However, the significant difference is the specular reflection geometry is dependent on the blaze angle,
, and NOT the grating surface normal. This results in the ability to change the diffraction efficiency by only changing the blaze angle of the diffraction grating.
The 0th order reflection from a blazed grating is shown in Figure 4. The incident light at angle is reflected at
for
= 0. From Eq. 3, the only solution is
= –
. This is analogous to specular reflection from a flat surface.
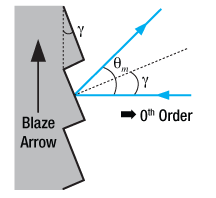
Figure 6. Blazed Grating, Incident Light Normal to Grating Surface
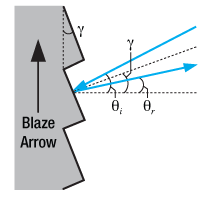
Figure 5. Blazed Grating, Specular Reflection from Facet
The specular reflection from the blazed grating is different from the flat surface due to the surface structure, as shown in Figure 5. The specular reflection, , from a blazed grating occurs at the blaze angle geometry. This angle is defined as being negative if it is on the same side of the grating surface normal as
. Performing some simple geometric conversions, one finds that
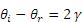
(4)
Figure 6 illustrates the specific case where = 0°, hence the incident light beam is perpendicular to the grating surface. In this case, the 0th order reflection also lies at 0°. Utilizing Eqs. 3 and 4, we can find the grating equation at twice the blaze angle:
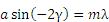
(5)
Littrow Configuration for Reflective Gratings
The Littrow configuration refers to a specific geometry for blazed gratings and plays an important role in monochromators and spectrometers. It is the angle at which the grating efficiency is the highest. In this configuration, the angle of incidence of the incoming and diffracted light are the same,
=
, and
> 0 so
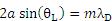
(6)
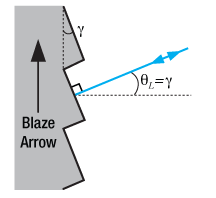
Figure 7. Littrow Configuration
The Littrow configuration angle, , is dependent on the most intense order (
= 1), the design wavelength,
, and the grating spacing
. It is easily shown that the Littrow configuration angle,
, is equal to the blaze angle,
, at the design wavelength. The Littrow / blaze angles for all Thorlabs' Blazed Gratings can be found in the grating specs tables.
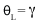
(7)
It is easily observed that the wavelength dependent angular separation increases as the diffracted order increases for light of normal incidence (for = 0°,
increases as
increases). There are two main drawbacks for using a higher order diffraction pattern over a low order one: (1) a decrease in efficiency at higher orders and (2) a decrease in the free spectral range,
![]() , defined as:
, defined as:
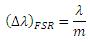
(8)
where is the central wavelength, and
is the order.
The first issue with using higher order diffraction patterns is solved by using an Echelle grating, which is a special type of ruled diffraction grating with an extremely high blaze angle and relatively low groove density. The high blaze angle is well suited for concentrating the energy in the higher order diffraction modes. The second issue is solved by using another optical element: grating, dispersive prism, or other dispersive optic, to sort the wavelengths/orders after the Echelle grating.
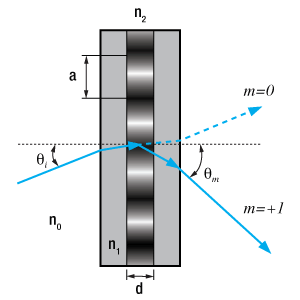
Figure 8. Volume Phase Holographic Grating
Volume Phase Holographic Transmission Gratings
Unlike traditional gratings, volume phase holographic (VPH) gratings do not have surface grooves. Instead, VPH gratings consist of a dichromated gelatin (DCG) film between two glass substrates. These VPH gratings are designed to reduce the periodic errors that can occur in blazed gratings. Surface gratings with high groove density also have an issue with polarization dependent loss. These unique transmission gratings deliver high first-order diffraction peak efficiency, low polarization dependence, and uniform performance over broad bandwidths.
The desired grating pattern is comprised of a repetitive series of lines separated by distance . The fringe planes for transmission gratings are perpendicular to the plane of the plate as seen in Figure 8, allowing any frequency of light to pass through the plate. Diffraction occurs as incoming light crosses through the DCG film. Therefore, the three major factors that determine performance are film thickness, bulk index (the average index of refraction between Bragg planes), and index modulation (the difference of index of refraction between the Bragg planes). The incident light enters the grating at an angle of
, as measured from the surface normal. The light of order
exiting the grating leaves at an angle of
, relative to the surface normal. The grating expression mentioned above can be used to calculate diffraction angles for volume phase holographic gratings since dispersion is based on the line density. The quality of the grating is determined by the fringe contrast, with a poor fringe contrast resulting in low efficiency or no grating at all.
The DCG film is taken through multiple quality control steps to ensure it performs up to standard and then cut into the desired size. The film is sealed between two glass covers to prevent degradation of the material. Since the DCG film is contained between two glass substrates, VPH gratings have high durability and long lifetimes, as well as easy maintenance compared to other gratings that can be easily damaged.
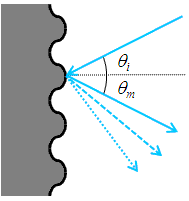
Figure 9. Holographic Grating
Holographic Surface Reflective Gratings
While blazed gratings offer extremely high efficiencies at the design wavelength, they suffer from periodic errors, such as ghosting, and relatively high amounts of scattered light, which could negatively affect sensitive measurements. Holographic gratings are designed specially to reduce or eliminate these errors. The drawback of holographic gratings compared to blazed gratings is reduced efficiency.
Holographic gratings are made from master gratings by similar processes to the ruled grating. The master holographic gratings are typically made by exposing photosensitive material to two interfering laser beams. The interference pattern is exposed in a periodic pattern on the surface, which can then be physically or chemically treated to expose a sinusoidal surface pattern. An example of a holographic grating is shown in Figure 9.
Please note that dispersion is based solely on the number of grooves per mm and not the shape of the grooves. Hence, the same grating equation can be used to calculate angles for holographic as well as ruled blazed gratings.
| Posted Comments: | |
user
(posted 2024-07-26 12:42:19.993) Is the data for the diffraction efficiency available in csv format or similar? cdolbashian
(posted 2024-08-02 11:40:16.0) Thank you for reaching out to us with this inquiry. I have contacted you directly to share the raw data from the graphs presented on the web. Zhou Li
(posted 2024-06-19 18:35:31.083) Hello, I would like to ask the following questions about this grating:
Can it be used with 1.5um lasers?
Does the diffraction efficiency become very low?
Can it be used in pulse compression systems in CPA? What is the damage threshold?
你好,我想咨询有关这款光栅的如下问题:
请问它能用于1.5um激光吗?
衍射效率会不会变得很低?
能被用在脉冲压缩系统中吗?损伤阈值大概多大? cdolbashian
(posted 2024-06-21 04:30:08.0) Thank you for reaching out to us with this inquiry. The efficiency curves vs. wavelength are shown on the product page within the individual specs tables. I am unclear on your second question regarding CPA, and have contacted you directly to discuss this. Finally, we do not have an official damage threshold spec for these gratings. user
(posted 2024-03-27 11:26:29.08) is this ruled gratings or replicated from ruled master? cdolbashian
(posted 2024-03-29 02:48:04.0) Thank you for reaching out to us. These are made with a ruled master. Kunhao Ji
(posted 2024-01-10 16:16:53.573) Hi Technical Team,
I would like to know the damage threshold of the ruled diffraction grating. Is it safe to use it for few Watts of average power with a beam size of 5mm?
Many thanks,
Kunhao jdelia
(posted 2024-01-23 03:21:52.0) Thank you for contacting Thorlabs. We unfortunately do not have an official damaged threshold specification for our gratings. I have reached out to you directly to discuss your application. Srinivas Varma Pericherla
(posted 2021-02-25 16:55:48.127) Hi,
I want to ask if you guys have ruled diffraction gratings for 830 & 970 nm with groove density 1800lp/mm and 50x50mm size. These are for the purpose of a 4f grating compressor system. Please let me know your product availability at these configurations.
Thanks. YLohia
(posted 2021-03-05 10:00:20.0) Hello, unfortunately, we do not stock such a diffraction grating at the moment. Custom items can be requested by using the "Request Quote" above or by emailing your local Thorlabs team (in your case, techsupport@thorlabs.com). We will discuss the possibility of offering this directly. Greg Lafyatis
(posted 2020-07-01 13:40:13.107) I would like to use one of your NIR gratings in a non-Littrow configuration and wondered how hard would it be to estimate the grating efficiency in the arrangement we are using. We could do a Hugens principle type estimation but would prefer something more sophisticated. Is his easy for you? YLohia
(posted 2020-07-14 04:57:13.0) Hello, thank you for contacting Thorlabs. Unfortunately, it is not quite straightforward to estimate the grating efficiency for these in a non-Littrow setting. If near-Littrow, the Littrow curves we provide will still be a relatively good indicator. Please note that if you do use a theoretical method to use a method to try and calculate efficiency, the math will most likely assume a perfect groove shape. Real world results rarely produce a perfectly shaped and completely smooth groove structure. While line spacing determines dispersion, groove shape, profile and any imperfections have a direct impact on the efficiency. Simon Roeder
(posted 2019-05-28 11:47:06.307) Hello,
I'm interested in the GR50-0610. I want to use two of them for pulse compression in an incident angle of 36° and a frequency range from 1024nm-1059nm.
I would be really grateful for an efficiency estimate. A plot similar to the one you provided for the blaze wavelength of 1000nm would be appretiated.
Regards
Simon Roeder YLohia
(posted 2019-06-28 10:21:58.0) Hello Simon, thank you for contacting Thorlabs. I have reached out to you directly with this data. liyonghong6
(posted 2017-08-16 11:28:23.113) can you offer the reflective grating which polarization
independent tfrisch
(posted 2017-09-07 09:24:46.0) Hello, thank you for contacting Thorlabs. Metal coatings will always have a difference in performance between the S and P polarization states. I will reach out to you directly about the needs of your application. |
Transmission Gratings
Thorlabs offers two types of transmission gratings: ruled and volume phase holographic. The ruled transmission gratings are created by scratching or etching a transparent substrate with a repetitive, parallel structure, creating areas where light can scatter. These gratings have a sawtooth diffraction profile and are made of epoxy and/or plastic imprints from a master copy, in a process called replication. Our volume phase holographic diffraction gratings consist of a dichromated gelatin (DCG) film between two glass substrates. These gratings have a sinusoidal wave diffraction pattern written on the DCG film using a laser setup. For more information, please refer to the Gratings Tutorial tab.
| Ruled Diffraction Gratings | ||
|---|---|---|
 |
UV | Thorlabs' ruled transmission gratings disperse incident light on the opposite side of the grating at a fixed angle. They are ruled and blazed for optimum efficiency in their respective wavelength range, are relatively polarization insensitive, and have an efficiency comparable to that of a reflection grating optimized for the same wavelength. They are ideal for applications that require fixed gratings such as spectrographs. |
| Visible | ||
| Near IR | ||
| UV Ruled Transmission Blazed Diffraction Gratings |
|---|
| Visible Ruled Transmission Blazed Diffraction Gratings |
|---|
| NIR Ruled Transmission Blazed Diffraction Gratings |
|---|
| Volume Phase Holographic Diffraction Gratings | |||
|---|---|---|---|
 |
Volume Phase Holographic | Thorlabs' volume phase holographic (VPH) gratings consist of a DCG film between two glass substrates. These unique transmission gratings are easy to maintain and deliver high first-order diffraction peak efficiency and uniform performance over broad bandwidths. | |
| Visible VPH Transmission Gratings |
|---|
| NIR VPH Transmission Gratings |
|---|
Reflective Gratings
Reflective grating master copies are made by depositing a metallic coating on an optic and ruling parallel grooves in the surface. Thorlabs' reflective gratings are made of epoxy and/or plastic imprints from a master copy, in a process called replication. In all cases, light is reflected off of the ruled surface at different angles corresponding to different orders and wavelengths. All of Thorlabs' ruled reflective diffraction gratings exhibit a sawtooth profile, also known as blazed, while our reflective holographic diffraction gratings exhibit a sinusoidal profile. For more information, please refer to the Gratings Tutorial tab.
| Ruled Diffraction Gratings | ||
|---|---|---|
 |
UV | Ruled gratings can achieve higher efficiencies than holographic gratings due to their blaze angles. They are ideal for applications centered near the blaze wavelength. Thorlabs offers replicated ruled diffraction gratings in a variety of sizes and blaze angles. |
| Visible | ||
| Near IR | ||
| Mid IR | ||
| UV Ruled Reflective Blazed Diffraction Gratings |
|---|
| Visible Ruled Reflective Blazed Diffraction Gratings |
|---|
| Near-IR Ruled Reflective Blazed Diffraction Gratings |
|---|
| Mid-IR Ruled Reflective Blazed Diffraction Gratings |
|---|
| Holographic Diffraction Gratings | |||
|---|---|---|---|
 |
Holographic | Holographic gratings have a low occurrence of periodic errors, which results in limited ghosting, unlike ruled gratings. The low stray light of these gratings makes them ideal for applications where the signal-to-noise ratio is critical, such as Raman Spectroscopy. | |
| Reflective Holographic Sinusoidal Diffraction Gratings |
|---|
| Echelle Diffraction Gratings | |||
|---|---|---|---|
 |
Echelle | Echelle gratings are low period gratings designed for use in high diffraction orders. They are generally used with a second grating or prism to separate overlapping diffracted orders. They are ideal for applications such as high-resolution spectroscopy. | |
| Echelle Ruled Blazed Diffraction Gratings |
|---|
Selecting a grating requires consideration of a number of factors, some of which are listed below:
Efficiency:
Ruled gratings generally have a higher efficiency than holographic gratings. Holographic grating tend to have a lower efficiency but a broader effective wavelength range. The efficiency of ruled gratings may be desirable in applications such as fluorescence excitation and other radiation-induced reactions.
Blaze Wavelength:
Ruled gratings have a sawtooth groove profile created by sequentially etching the surface of the grating substrate. As a result, they have a sharp peak efficiency around their blaze wavelength. Holographic gratings are harder to blaze, and tend to have a sinusoidal groove profile resulting in a less intense peak around the design wavelength. Applications centered around a narrow wavelength range could benefit from a ruled grating blazed at that wavelength.
Stray Light:
Due to a difference in how the grooves are made, holographic gratings have less stray light than ruled gratings. The grooves on a ruled grating are machined one at a time which results in a higher frequency of errors. Holographic gratings are made through a lithographic process, which generally creates smoother grating masters free of tool marks. Replicants made from these masters exhibit less stray light. Applications such as Raman spectroscopy, where signal-to-noise is critical, can benefit from the limited stray light of the holographic grating.
Resolving Power:
The resolving power of a grating is a measure of its ability to spatially separate two wavelengths. It is determined by applying the Rayleigh criteria to the diffraction maxima; two wavelengths are resolvable when the maxima of one wavelength coincides with the minima of the second wavelength. The chromatic resolving power (R) is defined by R = λ/Δλ = n*N, where Δλ is the resolvable wavelength difference, n is the diffraction order, and N is the number of grooves illuminated. Due to their low groove density, Echelle gratings provide high resolving power.
Polarization Dependence:
Surface gratings that have high groove densities also have an issue with polarization dependent loss, often with significantly lower efficiency when exposed to parallel- versus perpendicularly-polarized light. Volume phase holographic gratings are designed for applications that require low polarization dependent loss at higher spatial frequencies.
For further information about gratings and selecting the grating right for your application, please visit our Gratings Tutorial.
Caution for Gratings with Surface Grooves:
The surface of a diffraction grating with surface grooves can be easily damaged by fingerprints, aerosols, moisture or the slightest contact with any abrasive material. Gratings should only be handled when necessary and always held by the sides. Latex gloves or a similar protective covering should be worn to prevent oil from fingers from reaching the grating surface. Solvents will likely damage the grating's surface. No attempt should be made to clean a grating other than blowing off dust with clean, dry air or nitrogen. Scratches or other minor cosmetic imperfections on the surface of a grating do not usually affect performance and are not considered defects. Conversely, volume phase holographic gratings can be cleaned using standard optics cleaning procedures and have high durability.


 Products Home
Products Home











 Zoom
Zoom


 NIR Ruled Reflective Gratings
NIR Ruled Reflective Gratings