High-Precision Aspheres: CNC Polished, N-BK7 or S-LAH64 Substrate

- Ø10 mm to Ø100 mm Aspheric Lenses
- Uncoated and AR-Coated Options Available
- Numerical Apertures from 0.23 - 0.62
AL100200-A
Ø100 mm
AL50100-C
Ø50 mm
AL3026-B
Ø30 mm
In-Process Asphere Metrology Test Station with PGI Dimension 5XL Profilometer

Please Wait
| Common Specificationsa | |
|---|---|
| Clear Aperture (Collimation) | >90% of Diameter |
| Focal Length Deviation | ±1% |
| Sag Deviation | ±7.5 µm |
| Surface Irregularity of Convex Surface |
<3 Fringes (RMS) |
| Wavefront Error (RMS) | <0.5 µm |
| Surface Quality |
40-20 Scratch-Dig (Uncoated) 60-40 Scratch-Dig (AR Coated) |
| AR Coating Reflectance | Ravg < 0.5% |
| Precision Aspheric Lenses Selection Guide | ||
|---|---|---|
| Substrate Material | NA | Mount |
| UV Fused Silica | 0.142 - 0.145 | Unmounted |
| 0.142 - 0.145 | Mounted | |
| 0.65 | Unmounted | |
| N-BK7 / S-LAH64 | 0.23 - 0.62 | Unmounted |
| 0.23 - 0.55 | Mounted | |
| Zinc Selenide | 0.22 - 0.67 | Unmounted |
| Acylindrical Lenses | 0.45 - 0.54 | Unmounted |
| Axicons | - | Unmounted |
| Click on the red Document icon next to the item numbers below to access the Zemax file download. Our entire Zemax Catalog is also available. |
| Webpage Features | |
|---|---|
| Clicking this info icon below will open a window that contains specifications, a reference drawing, performance plots, and aspheric coefficients. | |
Features
- Ø10 mm to Ø100 mm Plano-Convex Aspheric Lenses
- Numerical Aperture Choices from 0.23 to 0.62
- Offered Uncoated or AR Coated from 350 - 700 nm, 650 - 1050 nm, or 1050 - 1700 nm
- CNC Precision Polish Enables High Optical Performance
- Mounted Precision Aspheres Also Available
Thorlabs' Precision Aspheric Lenses are manufactured using a computer numerical control (CNC) process. By using CNC machines to grind and polish each lens (as opposed to molding), it becomes possible to produce large-diameter (≥10 mm) aspheric lenses that still provide near-diffraction-limited performance. For example, 15 mm diameter, CNC-polished aspheric lenses typically provide 20X to 50X less wavefront error than molded lenses.
These aspheric lenses are optimized for focusing light incident on the aspheric side of the lens with minimal spherical aberration, although they can also be used for collimation when light is incident on the plano side. These Ø10 mm - Ø100 mm lenses are available with NAs ranging from 0.23 to 0.62. The low-NA (<0.3) options are well suited for applications that require a specific beam shape to be maintained, while the high-NA (>0.4) options provide high light-gathering ability (low f/#) while still minimizing spherical aberration.
The lenses are available uncoated or with both sides having a broadband AR coating that provides <0.5% average reflectance (per surface) in the 350 - 700 nm, 650 - 1050 nm, or 1050 - 1700 nm range. They are manufactured from either
For mounting these lenses within a lens tube assembly, Thorlabs offers standard retaining rings in a wide variety sizes. Extra-thick retaining rings are also available, which provide easier mounting for high-curvature lenses (see the Mounting Options tab for more information).
Optical Performance Verification
Each lens undergoes a rigorous verification procedure. Our metrology lab uses Zygo Verifire™, NewView™, and GPI™ interferometers to generate a three-dimensional map of the lens's optical surfaces in a contact-free geometry. In addition, a PGI Dimension 5XL profilometer allows for contact measurements of optics. These capabilities allow us to measure and maintain our specifications with far greater confidence than would otherwise be possible. Please see the Metrology tab for more information.
Custom Aspheric Lenses
Thorlabs' CNC-polished aspheric lenses are manufactured at the production facility housed in our headquarters in Newton, NJ. Our optics business unit has a wide breadth of manufacturing capabilities that allow us to offer a variety of custom optics for both OEM sales and low quantity one-off orders. Custom lens diameters, focal lengths, substrates, coatings, and mounting options are available with prices that are comparable to our stock offerings. For more information, please see the Custom Capabilities tab or contact Tech Sales to inquire about a custom order.
Other CNC-Polished Aspheres
Thorlabs also manufactures CNC-polished aspheric lenses fabricated from UV fused silica with NAs up to 0.145 in mounted and unmounted versions. These Ø1" high-precision lenses feature tighter tolerances than those sold on this page. Higher NA UV fused silica lenses are available in various diameters in unmounted versions. Please see the Selection Guide table to the right for our full selection of precision aspheric lenses.
MRF-Polished Aspheres
We also offer diffraction-limited, MRF-polished aspheres with minimal wavefront error. These lenses are free of spherical aberrations and offer the best single-element solution for many on-axis applications.
Transmission Data for S-LAH64 and N-BK7 Substrates

Click to Enlarge
Click Here for Raw Data
The graph above shows the transmission of a 10 mm thick S-LAH64 substrate.
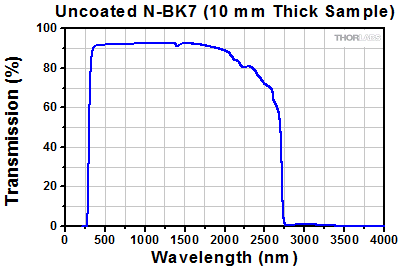 Click to Enlarge
Click to EnlargeClick Here for Raw Data
The graph above shows the transmission of a 10 mm thick N-BK7 substrate.
Reflectance Data for AR-Coated Lenses
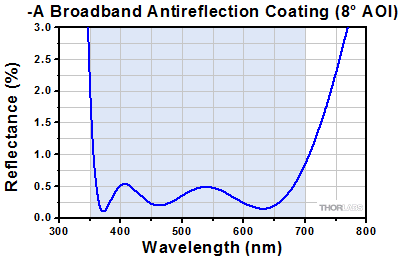
Click to Enlarge
Click Here for Raw Data
The blue shaded region indicates the specified 350 - 700 nm wavelength range where the specifications are guaranteed.
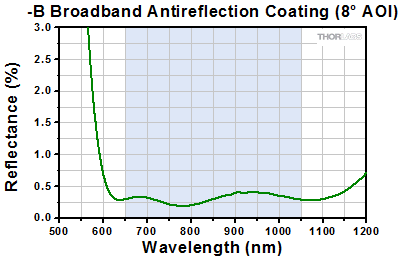
Click to Enlarge
Click Here for Raw Data
The blue shaded region indicates the specified 650 - 1050 nm wavelength range where the specifications are guaranteed.
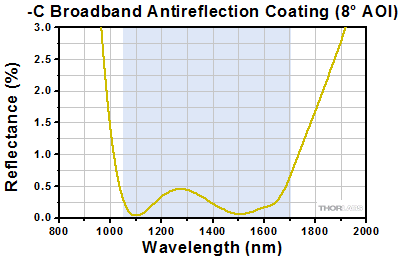
Click to Enlarge
Click Here for Raw Data
The blue shaded region indicates the specified 1050 - 1700 nm wavelength range where the specifications are guaranteed.
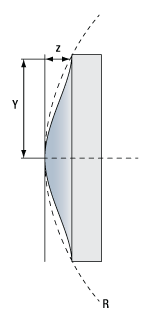
Click to Enlarge
Reference Drawing
Aspheric Lens Design Formula
| Definitions of Variables | |
|---|---|
| z | Sag (Surface Profile) as a Function of Y |
| Y | Radial Distance from Optical Axis |
| R | Radius of Curvature |
| k | Conic Constant |
| An | nth Order Aspheric Coefficient |
The aspheric surfaces of these lenses may be described using a polynomial expansion in Y, the radial distance from the optical axis. The surface profile or sagitta (often abbreviated as sag) is denoted by z, and is given by the following expression:
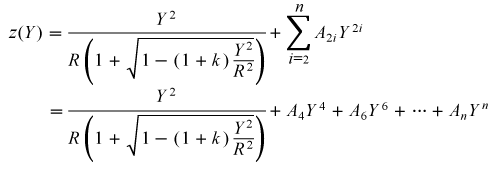
where R is the radius of curvature, k is the conic constant, and the An are the nth order aspheric coefficients. The sign of R is determined by whether the center of curvature for the lens surface is located to the right or left of the lens' vertex; a positive R indicates that the center of curvature is located to the right of the vertex, while a negative R indicates that the center of curvature is located to the left of the vertex. For example, the radius of curvature for the left surface of a biconvex lens would be specified as positive, while the radius of curvature for its right surface would be specified as negative.
Aspheric Lens Coefficients
Due to the rotational symmetry of the lens surface, only even powers of Y are contained in the polynomial expansion above. The target values of the aspheric coefficients for each product can be found by clicking either on the blue Info Icons in the tables below (![]() ) or on the red documents icon (
) or on the red documents icon (![]() ) next to each lens sold below.
) next to each lens sold below.
| Item # Prefix | Outer Diameter | EFL | Mounted Lenses | Suggested Fixed Lens Mount |
|---|---|---|---|---|
| AL108 | 10.0 mm | 8.0 mm | - | LMRA10 Combined with LMR18 (LMR18/M) |
| AL1210 | 12.5 mm | 10.0 mm | AL1210M, AL1210M-A, AL1210M-B, AL1210M-C |
LMR05 (LMR05/M) |
| AL1225 | 12.5 mm | 25.0 mm | AL1225M, AL1225M-A, AL1225M-B, AL1225M-C |
LMR05 (LMR05/M) |
| AL1512 | 15.0 mm | 12.0 mm | - | LMR15 (LMR15/M) |
| AL1815 | 18.0 mm | 15.0 mm | - | LMR18 (LMR18/M) |
| AL2018 | 20.0 mm | 18.0 mm | - | LMR20 (LMR20/M) |
| AL2520 | 25.0 mm | 20.0 mm | AL2520M, AL2520M-A, AL2520M-B, AL2520M-C |
LMR1 (LMR1/M) |
| AL2550 | 25.0 mm | 50.0 mm | AL2550M, AL2550M-A, AL2550M-B, AL2550M-C |
LMR1 (LMR1/M) |
| AL3026 | 30.0 mm | 26.0 mm | - | LMR30 (LMR30/M) |
| AL4532 | 45.0 mm | 32.0 mm | - | LMR45 (LMR45/M) |
| AL5040 | 50.0 mm | 40.0 mm | AL5040M, AL5040M-A, AL5040M-B, AL5040M-C |
LMR2 (LMR2/M) |
| AL50100 | 50.0 mm | 100.0 mm | AL50100M, AL50100M-A, AL50100M-B, AL50100M-C |
LMR2 (LMR2/M) |
| AL7560 | 75.0 mm | 60.0 mm | - | LMR3 (LMR3/M) or SM3L05 |
| AL75150 | 75.0 mm | 150.0 mm | - | LMR75 (LMR75/M) |
| AL100100 | 100.0 mm | 100.0 mm | - | LMR100 (LMR100/M) |
| AL100200 | 100.0 mm | 200.0 mm | - | LMR100 (LMR100/M) |
Thorlabs offers several mounting options for the aspheric lenses sold on this page. In addition, some of our precision aspheric lenses are available pre-mounted. The table at left shows suggested fixed lens mounts for each of our large-diameter aspheres and suggests equivalent mounted lenses where applicable. We also manufacture self-centering lens mounts that provide fast lens insertion and removal, capable of mounting all of the aspheres with diameters up to 50 mm as well as the AL75150.
Mounting Lenses Using Retaining Rings
Thorlabs' retaining rings are used to secure unmounted optics within lens tubes or optic mounts. These rings are secured in position using a compatible spanner wrench. For flat or low-curvature optics, standard retaining rings manufactured from anodized aluminum are available from Ø5 mm to Ø4". For high-curvature optics, extra-thick retaining rings are available in Ø1/2", Ø1", and Ø2" sizes.
Extra-thick retaining rings offer several features that aid in mounting high-curvature optics such as aspheric lenses, short-focal-length plano-convex lenses, and condenser lenses. As seen in the animation to the right, the guide flange of the spanner wrench will collide with the surface of high-curvature lenses when using a standard retaining ring, potentially scratching the optic. This contact also creates a gap between the spanner wrench and retaining ring, preventing the ring from tightening correctly. Extra-thick retaining rings provide the necessary clearance for the spanner wrench to secure the lens without coming into contact with the optic surface.
Aspheric Lens Metrology
Key Capabilities
- In Process Metrology for All CNC Polished Aspheres
- Non-Contact Interferometric and Non-Marring Profilometer Measurements
- Test Datasheets Available for OEM Sales and Custom Orders

Click to Enlarge
Zygo Verifire™ Asphere Interferometer Metrology Station
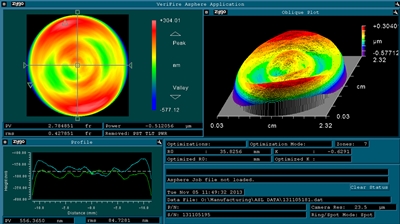
Click to Enlarge
Zygo Verifire™ Asphere Interferometer Results
In order to ensure that the specifications for our CNC lenses are continuously met, we utilize a variety of advanced metrology equipment for in-process measurements of lens shape, surface roughness, and transmitted wavefront error. First, a non-contact Zygo Verifire™ Asphere Interferometer is utilized to verify the surface profile of the lenses. This instrument operates as a Fizeau interferometer by varying the distance between a reference flat or sphere (consistent with ISO 10110-12 standards) and the optic under test. Reflections from each optical surface produce an interference pattern that is recorded by the diagnostic, resulting in measurements of the low-spatial-frequency components of the aspheric surface profile. This machine is mostly used on our diffraction-limited asphere line given its superior 3D accuracy.
An example of a surface irregularity measurement performed by a Zygo Verifire™ interferometer (λ = 633 nm) is shown below. It contains interference fringes at points where the surface profile of the reference does not match the finished asphere. The relatively smooth fringe profile across the >22 mm clear aperture of the lens (shown by the lineouts in the bottom left) demonstrates the extremely low sag deviation and surface irregularity of our lenses. The lens tested here has an exceptionally low RMS surface irregularity of 0.428 fringes over its entire clear aperture and a significantly better value around the center of the lens.
Complementary measurements of each optic's high-spatial-frequency surface roughness are then made with a Zygo NewView™ white light interferometer. This device operates with a reference in one arm of the interferometer and the aspheric optic in the other. The length of one arm is varied, resulting in a white light interferogram that carries information about finer details of the optical surface. Once the surface profile of an optic has been verified, a Zygo GPI LC™ interferometer is utilized to make measurements of the transmitted wavefront error through the lens. This test ensures that the bulk of the optic is free from defects and the rear surface of the lens is flat.
To further improve our metrology capabilities, a Taylor Hobson PGI Dimension 5XL profilometer has also been added to our lens cell. This instrument makes precision contact measurements by dragging a small stylus over the surface of an optic, resulting in a complete characterization of the surface profile. This method is extremely versatile, and it can be applied to optics with a high numerical aperture or large diameter that are unsuitable for interferometric measurements. As a result, we are able to produce custom aspheric lenses with specifications that significantly exceed the capabilities of other optics manufacturers. This machine is mostly used for in process metrology of aspheric grinding.
While all machines are in use, a Taylor Hobson LUPHOScan profilometer has been utilized for the bulk of the metrology. This non-contact surface profiler uses interferometry to perform ultra-precise 3D surface measurements with high, reproducible accuracy. This machine can provide specific data on radius and surface irregularities for our aspheres due to its unique balance of speed and accuracy.
Taken together, these interferometric and contact measurements produce a complete set of three-dimensional data for each aspheric lens. This detailed quality control information allows us to manufacture the highest quality of aspheres and maintain our specifications with an extremely high degree of confidence.

Click to Enlarge
Taylor Hobson PGI Dimension 5XL Profilometer Measuring an Aspheric Lens

Click to Enlarge
A Taylor Hobson PGI Dimension 5XL Profilometer allows for the production of large-diameter and high-numerical-aperture aspheric lenses, such as the piece to the left of the instrument.
Custom Aspheric Lenses
Key Capabilities
- Custom Lens Diameters, Focal Lengths, Substrates, Coatings, and Mounting Options
- Enhanced Specifications and Tighter Tolerances than Stock Optics
- Support for OEM Sales and Low-Quantity Special Orders

Click to Enlarge
A production lot of aspheric lenses that are ready for polishing at our headquarters in Newton, NJ.
Our in-house production capabilities allow us to offer a wide variety of custom CNC-polished and MRF-polished aspheric lenses. The diameter, focal length, conjugate ratio, substrate material, and coating of these optics can all be customized to meet the unique performance requirements of a given application. In addition, custom optics can be ordered with tighter tolerances and better specifications than our stock offerings. Because of our vertically integrated manufacturing process, these custom lenses are available for both OEM sales and individual low-quantity orders.
For the production of aspheric lenses, we have a CNC cell with Satisloh grinders and polishers, a QED Q-flex 100 for low wavefront error polishing, and a Satisloh C-25L for centration and custom shaping. The grinding and polishing machines allow us to manufacture both spherical and aspheric lenses with diameters from 2 mm (0.08") to 150 mm (5.91") (please contact Tech Sales with inquiries about even larger lenses). The centration machine can achieve centration down to 5 arcseconds, which is much tighter than the tolerance on most of our stock optics, and can also be used to create optics with custom shapes.
We are generally able to produce custom aspheric lenses with short lead times. For modifications to an existing part, delivery in one week is standard. For custom shapes and long focal length optics, a 6-8 week lead time is typical. To receive more information or a quote for a custom optic, please contact Tech Sales.

Click to Enlarge
An operator loading a Satisloh Centration Machine for stock aspheric optics and custom Lens Shapes.

Click to Enlarge
Satisloh Grinder for Aspheric Lenses

Click to Enlarge
QED Technologies Magnetorheological Finishing (MRF) Polisher
Our engineers are available to help manufacture optics for your application.
Customs are available in low quantities at prices that are comparable with our stock catalog products.
Please contact techsales@thorlabs.com with your custom optic requests.
| N-BK7 Damage Threshold Specifications | |
|---|---|
| Coating Designation (Item # Suffix) |
Damage Threshold |
| -A | 7.5 J/cm2 at 532 nm, 10 ns, 10 Hz, Ø0.504 mm |
| -B | 7.5 J/cm2 at 810 nm, 10 ns, 10 Hz, Ø0.144 mm |
| -C | 7.5 J/cm2 at 1542 nm, 10 ns, 10 Hz, Ø0.123 mm |
| S-LAH64 Damage Threshold Specifications | |
|---|---|
| Coating Designation (Item # Suffix) |
Damage Threshold |
| -A | 5 J/cm2 at 532 nm, 10 ns, 10 Hz, Ø0.345 mm |
| -B | 7.5 J/cm2 at 810 nm, 10 ns, 10 Hz, Ø0.155 mm |
| -C | 7.5 J/cm2 at 1064 nm, 10 ns, 10 Hz, Ø1.00 mm 7.5 J/cm2 at 1542 nm, 10 ns, 10 Hz, Ø0.246 mm |
Damage Threshold Data for Thorlabs' AR-Coated N-BK7 and S-LAH64 Aspheres
The specifications to the right are measured data for Thorlabs' AR-coated, CNC-polished N-BK7 and S-LAH64 precision aspheric lenses. Damage threshold specifications are constant for a given coating type, regardless of the size of the lens.
Laser Induced Damage Threshold Tutorial
The following is a general overview of how laser induced damage thresholds are measured and how the values may be utilized in determining the appropriateness of an optic for a given application. When choosing optics, it is important to understand the Laser Induced Damage Threshold (LIDT) of the optics being used. The LIDT for an optic greatly depends on the type of laser you are using. Continuous wave (CW) lasers typically cause damage from thermal effects (absorption either in the coating or in the substrate). Pulsed lasers, on the other hand, often strip electrons from the lattice structure of an optic before causing thermal damage. Note that the guideline presented here assumes room temperature operation and optics in new condition (i.e., within scratch-dig spec, surface free of contamination, etc.). Because dust or other particles on the surface of an optic can cause damage at lower thresholds, we recommend keeping surfaces clean and free of debris. For more information on cleaning optics, please see our Optics Cleaning tutorial.
Testing Method
Thorlabs' LIDT testing is done in compliance with ISO/DIS 11254 and ISO 21254 specifications.
First, a low-power/energy beam is directed to the optic under test. The optic is exposed in 10 locations to this laser beam for 30 seconds (CW) or for a number of pulses (pulse repetition frequency specified). After exposure, the optic is examined by a microscope (~100X magnification) for any visible damage. The number of locations that are damaged at a particular power/energy level is recorded. Next, the power/energy is either increased or decreased and the optic is exposed at 10 new locations. This process is repeated until damage is observed. The damage threshold is then assigned to be the highest power/energy that the optic can withstand without causing damage. A histogram such as that below represents the testing of one BB1-E02 mirror.

The photograph above is a protected aluminum-coated mirror after LIDT testing. In this particular test, it handled 0.43 J/cm2 (1064 nm, 10 ns pulse, 10 Hz, Ø1.000 mm) before damage.
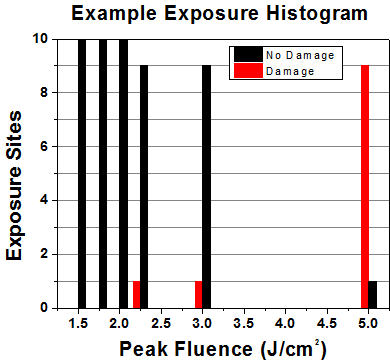
| Example Test Data | |||
|---|---|---|---|
| Fluence | # of Tested Locations | Locations with Damage | Locations Without Damage |
| 1.50 J/cm2 | 10 | 0 | 10 |
| 1.75 J/cm2 | 10 | 0 | 10 |
| 2.00 J/cm2 | 10 | 0 | 10 |
| 2.25 J/cm2 | 10 | 1 | 9 |
| 3.00 J/cm2 | 10 | 1 | 9 |
| 5.00 J/cm2 | 10 | 9 | 1 |
According to the test, the damage threshold of the mirror was 2.00 J/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.803 mm). Please keep in mind that these tests are performed on clean optics, as dirt and contamination can significantly lower the damage threshold of a component. While the test results are only representative of one coating run, Thorlabs specifies damage threshold values that account for coating variances.
Continuous Wave and Long-Pulse Lasers
When an optic is damaged by a continuous wave (CW) laser, it is usually due to the melting of the surface as a result of absorbing the laser's energy or damage to the optical coating (antireflection) [1]. Pulsed lasers with pulse lengths longer than 1 µs can be treated as CW lasers for LIDT discussions.
When pulse lengths are between 1 ns and 1 µs, laser-induced damage can occur either because of absorption or a dielectric breakdown (therefore, a user must check both CW and pulsed LIDT). Absorption is either due to an intrinsic property of the optic or due to surface irregularities; thus LIDT values are only valid for optics meeting or exceeding the surface quality specifications given by a manufacturer. While many optics can handle high power CW lasers, cemented (e.g., achromatic doublets) or highly absorptive (e.g., ND filters) optics tend to have lower CW damage thresholds. These lower thresholds are due to absorption or scattering in the cement or metal coating.
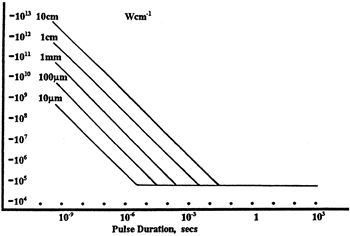
LIDT in linear power density vs. pulse length and spot size. For long pulses to CW, linear power density becomes a constant with spot size. This graph was obtained from [1].
Pulsed lasers with high pulse repetition frequencies (PRF) may behave similarly to CW beams. Unfortunately, this is highly dependent on factors such as absorption and thermal diffusivity, so there is no reliable method for determining when a high PRF laser will damage an optic due to thermal effects. For beams with a high PRF both the average and peak powers must be compared to the equivalent CW power. Additionally, for highly transparent materials, there is little to no drop in the LIDT with increasing PRF.
In order to use the specified CW damage threshold of an optic, it is necessary to know the following:
- Wavelength of your laser
- Beam diameter of your beam (1/e2)
- Approximate intensity profile of your beam (e.g., Gaussian)
- Linear power density of your beam (total power divided by 1/e2 beam diameter)
Thorlabs expresses LIDT for CW lasers as a linear power density measured in W/cm. In this regime, the LIDT given as a linear power density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size, as demonstrated by the graph to the right. Average linear power density can be calculated using the equation below.
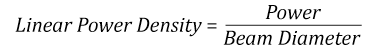
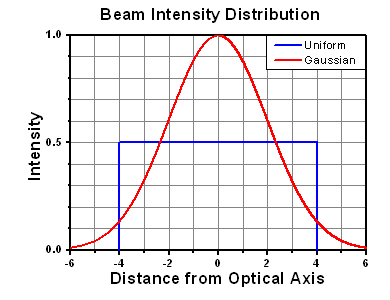
The calculation above assumes a uniform beam intensity profile. You must now consider hotspots in the beam or other non-uniform intensity profiles and roughly calculate a maximum power density. For reference, a Gaussian beam typically has a maximum power density that is twice that of the uniform beam (see lower right).
Now compare the maximum power density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately. A good rule of thumb is that the damage threshold has a linear relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 10 W/cm at 1310 nm scales to 5 W/cm at 655 nm):

While this rule of thumb provides a general trend, it is not a quantitative analysis of LIDT vs wavelength. In CW applications, for instance, damage scales more strongly with absorption in the coating and substrate, which does not necessarily scale well with wavelength. While the above procedure provides a good rule of thumb for LIDT values, please contact Tech Support if your wavelength is different from the specified LIDT wavelength. If your power density is less than the adjusted LIDT of the optic, then the optic should work for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. The damage analysis will be carried out on a similar optic (customer's optic will not be damaged). Testing may result in additional costs or lead times. Contact Tech Support for more information.
Pulsed Lasers
As previously stated, pulsed lasers typically induce a different type of damage to the optic than CW lasers. Pulsed lasers often do not heat the optic enough to damage it; instead, pulsed lasers produce strong electric fields capable of inducing dielectric breakdown in the material. Unfortunately, it can be very difficult to compare the LIDT specification of an optic to your laser. There are multiple regimes in which a pulsed laser can damage an optic and this is based on the laser's pulse length. The highlighted columns in the table below outline the relevant pulse lengths for our specified LIDT values.
Pulses shorter than 10-9 s cannot be compared to our specified LIDT values with much reliability. In this ultra-short-pulse regime various mechanics, such as multiphoton-avalanche ionization, take over as the predominate damage mechanism [2]. In contrast, pulses between 10-7 s and 10-4 s may cause damage to an optic either because of dielectric breakdown or thermal effects. This means that both CW and pulsed damage thresholds must be compared to the laser beam to determine whether the optic is suitable for your application.
| Pulse Duration | t < 10-9 s | 10-9 < t < 10-7 s | 10-7 < t < 10-4 s | t > 10-4 s |
|---|---|---|---|---|
| Damage Mechanism | Avalanche Ionization | Dielectric Breakdown | Dielectric Breakdown or Thermal | Thermal |
| Relevant Damage Specification | No Comparison (See Above) | Pulsed | Pulsed and CW | CW |
When comparing an LIDT specified for a pulsed laser to your laser, it is essential to know the following:
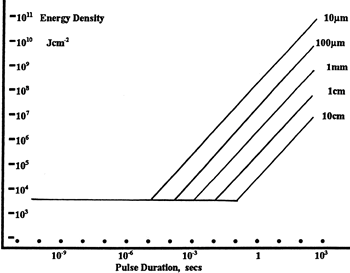
LIDT in energy density vs. pulse length and spot size. For short pulses, energy density becomes a constant with spot size. This graph was obtained from [1].
- Wavelength of your laser
- Energy density of your beam (total energy divided by 1/e2 area)
- Pulse length of your laser
- Pulse repetition frequency (prf) of your laser
- Beam diameter of your laser (1/e2 )
- Approximate intensity profile of your beam (e.g., Gaussian)
The energy density of your beam should be calculated in terms of J/cm2. The graph to the right shows why expressing the LIDT as an energy density provides the best metric for short pulse sources. In this regime, the LIDT given as an energy density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size. This calculation assumes a uniform beam intensity profile. You must now adjust this energy density to account for hotspots or other nonuniform intensity profiles and roughly calculate a maximum energy density. For reference a Gaussian beam typically has a maximum energy density that is twice that of the 1/e2 beam.
Now compare the maximum energy density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately [3]. A good rule of thumb is that the damage threshold has an inverse square root relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 1 J/cm2 at 1064 nm scales to 0.7 J/cm2 at 532 nm):
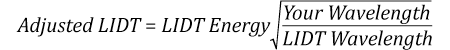
You now have a wavelength-adjusted energy density, which you will use in the following step.
Beam diameter is also important to know when comparing damage thresholds. While the LIDT, when expressed in units of J/cm², scales independently of spot size; large beam sizes are more likely to illuminate a larger number of defects which can lead to greater variances in the LIDT [4]. For data presented here, a <1 mm beam size was used to measure the LIDT. For beams sizes greater than 5 mm, the LIDT (J/cm2) will not scale independently of beam diameter due to the larger size beam exposing more defects.
The pulse length must now be compensated for. The longer the pulse duration, the more energy the optic can handle. For pulse widths between 1 - 100 ns, an approximation is as follows:
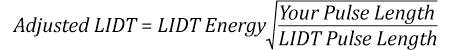
Use this formula to calculate the Adjusted LIDT for an optic based on your pulse length. If your maximum energy density is less than this adjusted LIDT maximum energy density, then the optic should be suitable for your application. Keep in mind that this calculation is only used for pulses between 10-9 s and 10-7 s. For pulses between 10-7 s and 10-4 s, the CW LIDT must also be checked before deeming the optic appropriate for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. Contact Tech Support for more information.
[1] R. M. Wood, Optics and Laser Tech. 29, 517 (1998).
[2] Roger M. Wood, Laser-Induced Damage of Optical Materials (Institute of Physics Publishing, Philadelphia, PA, 2003).
[3] C. W. Carr et al., Phys. Rev. Lett. 91, 127402 (2003).
[4] N. Bloembergen, Appl. Opt. 12, 661 (1973).
In order to illustrate the process of determining whether a given laser system will damage an optic, a number of example calculations of laser induced damage threshold are given below. For assistance with performing similar calculations, we provide a spreadsheet calculator that can be downloaded by clicking the button to the right. To use the calculator, enter the specified LIDT value of the optic under consideration and the relevant parameters of your laser system in the green boxes. The spreadsheet will then calculate a linear power density for CW and pulsed systems, as well as an energy density value for pulsed systems. These values are used to calculate adjusted, scaled LIDT values for the optics based on accepted scaling laws. This calculator assumes a Gaussian beam profile, so a correction factor must be introduced for other beam shapes (uniform, etc.). The LIDT scaling laws are determined from empirical relationships; their accuracy is not guaranteed. Remember that absorption by optics or coatings can significantly reduce LIDT in some spectral regions. These LIDT values are not valid for ultrashort pulses less than one nanosecond in duration.

A Gaussian beam profile has about twice the maximum intensity of a uniform beam profile.
CW Laser Example
Suppose that a CW laser system at 1319 nm produces a 0.5 W Gaussian beam that has a 1/e2 diameter of 10 mm. A naive calculation of the average linear power density of this beam would yield a value of 0.5 W/cm, given by the total power divided by the beam diameter:
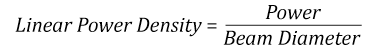
However, the maximum power density of a Gaussian beam is about twice the maximum power density of a uniform beam, as shown in the graph to the right. Therefore, a more accurate determination of the maximum linear power density of the system is 1 W/cm.
An AC127-030-C achromatic doublet lens has a specified CW LIDT of 350 W/cm, as tested at 1550 nm. CW damage threshold values typically scale directly with the wavelength of the laser source, so this yields an adjusted LIDT value:

The adjusted LIDT value of 350 W/cm x (1319 nm / 1550 nm) = 298 W/cm is significantly higher than the calculated maximum linear power density of the laser system, so it would be safe to use this doublet lens for this application.
Pulsed Nanosecond Laser Example: Scaling for Different Pulse Durations
Suppose that a pulsed Nd:YAG laser system is frequency tripled to produce a 10 Hz output, consisting of 2 ns output pulses at 355 nm, each with 1 J of energy, in a Gaussian beam with a 1.9 cm beam diameter (1/e2). The average energy density of each pulse is found by dividing the pulse energy by the beam area:
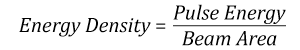
As described above, the maximum energy density of a Gaussian beam is about twice the average energy density. So, the maximum energy density of this beam is ~0.7 J/cm2.
The energy density of the beam can be compared to the LIDT values of 1 J/cm2 and 3.5 J/cm2 for a BB1-E01 broadband dielectric mirror and an NB1-K08 Nd:YAG laser line mirror, respectively. Both of these LIDT values, while measured at 355 nm, were determined with a 10 ns pulsed laser at 10 Hz. Therefore, an adjustment must be applied for the shorter pulse duration of the system under consideration. As described on the previous tab, LIDT values in the nanosecond pulse regime scale with the square root of the laser pulse duration:
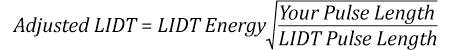
This adjustment factor results in LIDT values of 0.45 J/cm2 for the BB1-E01 broadband mirror and 1.6 J/cm2 for the Nd:YAG laser line mirror, which are to be compared with the 0.7 J/cm2 maximum energy density of the beam. While the broadband mirror would likely be damaged by the laser, the more specialized laser line mirror is appropriate for use with this system.
Pulsed Nanosecond Laser Example: Scaling for Different Wavelengths
Suppose that a pulsed laser system emits 10 ns pulses at 2.5 Hz, each with 100 mJ of energy at 1064 nm in a 16 mm diameter beam (1/e2) that must be attenuated with a neutral density filter. For a Gaussian output, these specifications result in a maximum energy density of 0.1 J/cm2. The damage threshold of an NDUV10A Ø25 mm, OD 1.0, reflective neutral density filter is 0.05 J/cm2 for 10 ns pulses at 355 nm, while the damage threshold of the similar NE10A absorptive filter is 10 J/cm2 for 10 ns pulses at 532 nm. As described on the previous tab, the LIDT value of an optic scales with the square root of the wavelength in the nanosecond pulse regime:
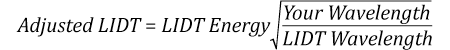
This scaling gives adjusted LIDT values of 0.08 J/cm2 for the reflective filter and 14 J/cm2 for the absorptive filter. In this case, the absorptive filter is the best choice in order to avoid optical damage.
Pulsed Microsecond Laser Example
Consider a laser system that produces 1 µs pulses, each containing 150 µJ of energy at a repetition rate of 50 kHz, resulting in a relatively high duty cycle of 5%. This system falls somewhere between the regimes of CW and pulsed laser induced damage, and could potentially damage an optic by mechanisms associated with either regime. As a result, both CW and pulsed LIDT values must be compared to the properties of the laser system to ensure safe operation.
If this relatively long-pulse laser emits a Gaussian 12.7 mm diameter beam (1/e2) at 980 nm, then the resulting output has a linear power density of 5.9 W/cm and an energy density of 1.2 x 10-4 J/cm2 per pulse. This can be compared to the LIDT values for a WPQ10E-980 polymer zero-order quarter-wave plate, which are 5 W/cm for CW radiation at 810 nm and 5 J/cm2 for a 10 ns pulse at 810 nm. As before, the CW LIDT of the optic scales linearly with the laser wavelength, resulting in an adjusted CW value of 6 W/cm at 980 nm. On the other hand, the pulsed LIDT scales with the square root of the laser wavelength and the square root of the pulse duration, resulting in an adjusted value of 55 J/cm2 for a 1 µs pulse at 980 nm. The pulsed LIDT of the optic is significantly greater than the energy density of the laser pulse, so individual pulses will not damage the wave plate. However, the large average linear power density of the laser system may cause thermal damage to the optic, much like a high-power CW beam.
| Posted Comments: | |
Suwan Kang
(posted 2024-04-01 15:33:23.28) Dear whom may concern,
I want to ask the CW Damage threshold and wavefront error for
AL2550-B in 852nm and
AL5040-B in 850nm.
We look forward to your reply.
Thank you.
Best regards,
Suwan Kang. jdelia
(posted 2024-04-04 02:32:59.0) Thank you for contacting Thorlabs. Since we have not measured a CW damage threshold for our -B coated N-BK7 and S-LAH64 aspheres, I have reached out to you directly to ask for the specifications of your beam so that we may look into whether we believe it would be suitable for these lenses. For both of the optics you mentioned, we specify an RMS wavefront error <0.5 µm. Kirsten Kanneworff
(posted 2023-10-05 13:27:37.623) Dear Thorlabs,
We have a question on the tab about the Lens equation. For all lenses the radius of curvature R and the aspheric coefficients. However only for R the units are given. However, what the units of the aspheric coefficients and of the Radial Distance from Optical Axis Y for this equation? We would like to be sure of this to understand the operation of our spherical lens.
Kind regards,
Kirsten Kanneworff cdolbashian
(posted 2023-10-19 10:34:54.0) Than you for reaching out to us with this inquiry. Using some dimensional analysis, it can be shown that the units for Y are also in mm, and each of the coefficients has an exponent which is 1 less than the power of the order of the expansion term, and also the units are [1/mm], rather than mm. I have contacted you directly to discuss this in more detail. Gregoire Vallet
(posted 2022-02-04 07:59:36.427) Dear Thorlabs personal,
I am looking for 1" diam f = 50 mm lenses that could withstand long illumination (several hours) by a 30 W cw laser @ 900 nm.
This means an average of about 70 kW/m^2.
Would standard lenses hold on (a find only the pulsed damaging threshold on the page...)?
Thank you in advance,
wishing you a pleasant afternoon,
Gregoire cdolbashian
(posted 2022-02-09 04:54:03.0) Thank you for reaching out to us at Thorlabs Gregoire! Based on the fact that you have a beam with a linear density of only about ~25W/cm (converted from m^2-->
cm). Our -B coating can withstand much higher intensities than this. We don't anticipate any problems with your particular configuration. Hui Li
(posted 2021-07-20 15:40:14.02) This lens does not fit in SM2AD45 YLohia
(posted 2021-07-21 03:16:45.0) Hello, thank you for contacting Thorlabs. The M45.5x0.5 threading on the SM2AD45 has a minimum minor diameter (the absolute smallest diameter of the internal threading) of 44.959 mm, so there is a very slim chance that the two parts do not fit. It is likely the tolerancing is very close in your case compared to the other components you have. Please measure the internal diameter of the SM2AD45 and the outer diameter of the AL4532 with a caliper. We suggest making sure the optic doesn't tilt as it is inserted in the adapter. We have reached out to you directly to troubleshoot further. Nery Solana
(posted 2021-05-10 05:28:41.357) Hello,
Taking into account that you use S-LAH64 as lense substrate, I was wandering whether you know this material has been used for space uses. I would appreciate your comments on that.
Thank you very much cdolbashian
(posted 2021-09-01 01:56:37.0) Thank you for reaching out to us at Thorlabs. Assuming you are inquiring about the use of these lenses in outer space, we do not have this data. I have contacted you directly to inquire about other environmental factors which may narrow down the feasibility of using this material in space. Van Rudd
(posted 2020-12-03 11:58:38.33) Is the "working distance" in the specifications the same as the "back focal length" in the reference diagrams? YLohia
(posted 2020-12-04 10:22:09.0) Thank you for contacting Thorlabs. Yes, the "working distance" spec is the same as the "back focal length" reference callout. user
(posted 2020-09-25 14:26:21.28) Hi, I have a slight confusion related to the Transmission Data for S-LAH64 and N-BK7 Substrates section. On the "transmission (%)" graphs, are those values the Fresnel's transmission coefficients or the transmittances? Thanks YLohia
(posted 2020-09-28 11:53:40.0) Hello, the transmission graphs display the transmission percentage of light (as a function of wavelength) through a 10 mm thick uncoated piece of glass. This includes losses due to Fresnel reflections. Maxime Joos
(posted 2020-01-03 15:24:31.573) Dear,
I am deceived by the optical performance of this product (AL1225-A).
Used as a fiber outcoupler, the output intensity profile looks terrible (probably artifacts from the CNC machining). The wavefronts are aberrated (around 0.5 micron peak-to-peak) which is apparently within the specifications (according to customer service) but definitely not enough for my application (fiber outcoupling).
Similar product from the competitor does not have this wavefront distortion issue.
Maxime Joos nbayconich
(posted 2020-01-16 08:00:05.0) Thank you for contacting Thorlabs. We specify our CNC polished aspheres as near diffraction limited, due to the CNC machining process these types of lenses cannot be considered a true diffraction limited lenses as the MRF polished aspheres. An MRF polished lens may be a better option for your application.
Would it be possible to provide more details of the type lens you purchased for comparison?
I have reached out to you directly to discuss your application in more detail. levi.liad
(posted 2019-03-04 04:41:24.057) Hi
we are looking for the CW LIDT for this product which we have purchased from you.
AL100200-B - Ø100 mm N-BK7 Aspheric Lens, f=200 mm, NA=0.23, ARC: 650-1050 nm
the only thing I see is the Pulsed Laser LIDT.
can you please driect me to this number.
It is supposed to be in units of Linear Power density W/cm2.
thx
Liad YLohia
(posted 2019-04-05 12:14:24.0) Hello Liad, we received your email and have been in direct contact with you regarding this. rbjaculbia
(posted 2018-07-02 22:22:51.163) I would like to ask if it is possible to modify the diameter of AL2018 from 20mm to 11mm. Thanks! YLohia
(posted 2018-07-03 12:25:57.0) Hello, we generally have the ability to offer smaller sizes of stock lenses. Please contact techsupport@thorlabs.com for such quotes. user
(posted 2016-10-24 13:22:35.46) Would be useful to have asphere options with EFL = 75mm and 125mm to fill in the gaps you have in the BK7 line. Also useful would be UVFS substrates. tfrisch
(posted 2016-10-25 11:41:14.0) Hello, thank you for contacting Thorlabs. While we are able to offer custom lenses through our Tech Support (TechSupport@Thorlabs.com), we understand the need for stock items as well. I've posted your suggestions in our internal engineering forum. Thank you. louis.desbiens
(posted 2016-02-10 20:34:03.82) What is the CW LIDT for those lenses ? (N-BK7 and S-LAH64)
thanks ! besembeson
(posted 2016-03-03 11:38:30.0) Response from Bweh at Thorlabs USA: We don't have such CW damage thresholds for these at the moment. With your laser characteristics provided via email, I can recommend suitability. user
(posted 2014-11-22 15:17:03.653) With Strehl being around 0.1 this is far away from diffraction limited focusing! And the optical design is supposed to be diffraction limited, that's kind of the definition of an asphere.
Stating that the design is diffraction limited and not talking about real life performance seems like cheating to me. besembeson
(posted 2014-12-11 05:51:48.0) Response from Bweh at Thorlabs USA: Strehl ratio of 0.1 is obviously not anywhere near diffraction limit. I am curious to know where this number comes from though since we don't typically specify this as it is not very commonly used. In general, you associate the term "diffraction limit" to an optical component when the Strehl ratio is around 0.8. But like I mentioned, the design is diffraction limited and the performance is indeed near-diffraction-limit. If you provide me your email, I can look further into the parameters of any particular lens that you are interested in, and possibly provide you with a sample to test in your system. You can contact me at techsupport@thorlabs.com. user
(posted 2014-10-02 21:47:18.357) Concerning the question on 2014-03-17 15:40:27.253:
These aspheres are manufactures with an irregularity of < 3fr.RMS as stated on the overview. If you want a diffration limited focus you need to get below 1.5fr PV! So the not matching coating is nothing to worry about. The focusing behaviour of these lenses is quite constant through the VIS and NIR, talking about Strehl < 0.1, but still better than a sphere. besembeson
(posted 2014-11-14 12:10:30.0) Response from Bweh at Thorlabs USA: Yes that is correct that these lenses are not diffraction limited with the <3 fringes of surface irregularity in terms of performance and that is why we say "near-diffraction-limit performance". But the design is diffraction limited. max.schiller
(posted 2014-09-18 13:52:11.183) Hi, how high is the laser-induced damage threshold for the AL1210-B? Max. jlow
(posted 2014-09-25 02:58:42.0) Response from Jeremy at Thorlabs: We are testing these for laser damage threshold and we will post the numbers once testing has finished. dkahn
(posted 2014-07-22 14:57:33.947) Please advise on typical PSF at the design wavelength, assuming a uniform incoming collimated beam of 46 mm diameter.
David jlow
(posted 2014-08-01 02:45:15.0) Response from Jeremy at Thorlabs: We provide the Zemax files for modeling these CNC aspheres on our website. You can load the Zemax file and find the PSF for your specific lens. tetsu.takekoshi
(posted 2014-06-30 19:02:56.597) Hello,
We have tried using this lens (AL2520) in a microscope configuration to collimate a 0.11 NA beam from a single mode fiber and refocus using a 300mm spherical singlet. The most important thing for us is beamshape and I realize this may not be the right lens (triplet is perhaps better?). The beam looks very non-Gaussian away from the focus.
What is responsible for this exactly? Using Zemax everything seems to be extremely Gaussian near the focus spot and at intermediate points. Is the rms wavefront distortion spec quoted (<0.5 um) due mainly to manufacturing errors? We have also tried a lower NA version (AL1225) as suggested in your overview but get similar results on the bench. jlow
(posted 2014-07-14 11:19:15.0) Response from Jeremy at Thorlabs: It's hard to comment on this without the details of your setup. We will contact your directly to get the details of your setup and the results you are seeing and troubleshoot this further. user
(posted 2014-03-17 15:40:27.253) Why in the world would you sell aspheres with AR coatings from 350-700nm if the lenses are optimized for 780nm? A diffraction limited asphere designed for use at 780nm is virtually useless at visible wavelengths. jlow
(posted 2014-03-19 02:02:38.0) Response from Jeremy at Thorlabs: The lens, while designed for 780nm, can still achieve diffraction-limited or near-diffraction-limited performance in the visible. This can be verified with any commercial optical design software, such as Zemax. |




 Products Home
Products Home












 Unmounted N-BK7 / S-LAH64 Aspheres
Unmounted N-BK7 / S-LAH64 Aspheres