Axicons, UV Fused Silica
- Transforms a Collimated Beam into a Ring
- Apex Rounding Diameter: <1.5 mm
- Uncoated or AR Coated Options Available
AX2520-B
650 - 1050 nm, Ø1"
AX251-UV
245 - 400 nm, Ø1"
AX125-C
1050 - 1700 nm, Ø1/2"
Application Idea
AX2520-B Prism in a CP35 Cage Plate
AX2540-A
350 - 700 nm, Ø1"

Please Wait
| Common Specifications | |
|---|---|
| Substrate Material | UV Fused Silicaa |
| Diameter | 1/2" (12.7 mm) or 1" (25.4 mm) |
| Diameter Tolerance | +0.0 / -0.1 mm |
| Apex Rounding Diameter (S1) | <1.5 mm |
| Surface Quality (S1, S2) | 40-20 Scratch-Dig |
| Surface Flatness (S2) | <λ/10 at 633 nm |
| Surface Deviation (RMS) (S1) | <0.05 µm |
| Surface Roughness (RMS) (S1) | <6 Å |
| Clear Aperture (S1, S2) | >90% of Diameter |
| Edge Thickness | 5.0 mm |
| Edge Thickness Tolerance | +0.1/-0.0 mm |
| Center Thickness Tolerance | +0.1/-0.0 mm |
| Angular Tolerance | ±0.01° |
Click to Enlarge
The diagram above shows the definitions of thicknesses and angles used on this page.
Features
- 1/2" and 1" Diameters Available
- Physical Angles Available: 0.5°, 1.0°, 2.0°, 5.0°, 10.0°, 20.0°, and 40.0°
- Offered Uncoated or With an AR Coating
Applications
- Laser Drilling/Optical Trepanning
- Optical Trapping
- Optical Coherence Tomography (OCT)
- Corneal Surgery
- Telescopes
An axicon, also known as a rotationally symmetric prism, is a lens that features one conical surface and one plano surface. They are commonly used to create a beam with a Bessel intensity profile or a conical, non-diverging beam. When converting a collimated beam into a ring, the plano side of the axicon should face the collimated source.
An axicon deflects light according to Snell's Law, which can be used to find the deflection angle:
where n is the index of refraction of the glass, α is the physical angle of the prism, and ß is the angle the deflected beam creates with the optical axis. Here, the refractive index of air is assumed to be 1. This interaction is illustrated in the reference image to the right. For more information, please see the Beam Shape tab above.
These precision-polished axicons are offered with physical angles from 0.5° to 40°. These axicons are precisely manufactured from high-quality UV Fused Silica, making them ideally suited for high-power laser applications. Our axicons are offered uncoated or with an antireflection coating deposited on both sides for one of four wavelength ranges: -UV (245 - 400 nm), -A (350 - 700 nm), -B (650 - 1050 nm), or -C (1050 -1700 nm). These coatings reduce surface reflections from the lens to maximize transmission (Ravg < 0.5%). For a custom coating, please contact Tech Support for a quote.
Custom Axicons
Thorlabs' Fused Silica Axicons are manufactured at the production facility in our headquarters in Newton, NJ. In-house manufacturing allows for full control over the production process, resulting in minimal apex rounding diameter. For more information, see the Beam Shape tab. Our optics business unit has a wide breadth of manufacturing capabilities that allow us to offer a variety of custom optics for both OEM sales and low quantity one-off orders. Custom physical angles and coatings are available with prices that are comparable to our stock offerings. Utilizing a unique, post-polishing process, we are able to offer Apex Rounding Diameters down to 0.7 mm and Surface Irregularities as low as 10 nm (RMS). Please contact Tech Support to inquire about custom orders.
Thorlabs also offers Zinc Selenide Axicons with a broadband AR coating for 7 - 12 µm.
|
 |
 |
Axicon Beams
- Bessel Beam: Non-Diffracting
- Ring-Shaped Beam: Ideal for Laser Drilling
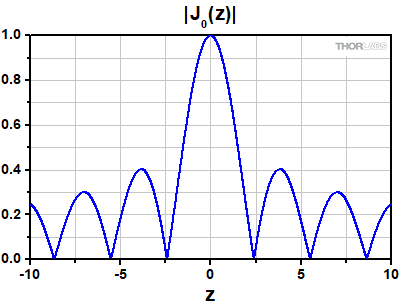
Figure 1: The absolute value of a 0th order Bessel function. A true Bessel Beam requires each ring to have the same energy as the central peak, thus an infinite amount of energy is needed.
A Bessel beam is a non-diffracting beam of concentric rings, each having the same power as the central ring. Technically, a Bessel beam cannot be created as it requires infinite energy. A beam closely resembling a Bessel distribution can be generated by passing a Gaussian beam through an axicon and taking the projection of the beam close to the axicon’s conical surface. The absolute value of a 0th order Bessel function of the first kind is shown in Figure 1 (right).
When the beam is projected further from the lens, a single ring-shaped beam is formed. The beam is actually conical (i.e., diameter increases with distance), but the rays are non-diverging so that the thickness of the ring remains constant (see Figure 2). The ring's thickness will be half of the input laser beam's diameter. This type of beam is commonly used in laser-drilling applications.
Figure 2: Axicon ray tracing diagram.
Apex Rounding
The intensity distributions of the resulting Bessel and ring-shaped Gaussian beams are influenced by tip imperfections. The central lobe of the zero-order Bessel beam shows intensity oscillations rather than spatial invariance1 if the tip is rounded, while the hollow Gaussian beam features an asymmetric ring with a tail towards the center or secondary rings2. To minimize apex rounding, Thorlabs manufactures axicons in-house. This allows for full control over the production process, resulting in a minimum apex rounding diameter of 0.70 mm.
Figure 4: Ring-shaped beams as seen on a viewing screen for the Thorlabs axicon (top) and two generic axicons (middle; bottom). The ring generated by the Thorlabs axicon transitions from high to low intensity over a short range, while the generic axicons make the transition over more pixels. The white horizontal line indicates the location of the extracted intensity profiles in the graph below.
Since any imperfections in the axicon tip will influence the properties of the output beam, we demonstrate the quality of our Thorlabs axicons by comparing the resulting hollow Gaussian beam to those produced by two generic axicons. The ring-shaped beam can be created by using the experimental setup shown in Figure 3, which includes a 633 nm laser, GBE05-A 5X achromatic Galilean beam expander, an SM2D25D SM2 ring-actuated iris, the axicon (AX2520 and two generic axicons with a physical angle of 20°), and an EDU-VS1 polystyrene viewing screen. For optimal performance, the laser incident on the axicon must have a collimated, small diameter beam. This is achieved by expanding a collimated beam and then passing the beam through an iris closed to 2.0 mm. The resulting beam shape is then projected onto the viewing screen, which is positioned in the far-field. For ease of translation, the screen was mounted onto a dovetail optical rail with a snap-on rail carrier.
Figure 4 shows images of the resulting ring-shaped Gaussian beams visible on the viewing screen from the three tested axicons. Qualitatively, the Thorlabs axicon (Figure 4, top) produces a clean ring with high contrast between the ring edge and the dark center. The axicons from other manufacturers, however, produce rings of varying quality. One of the generic axicons, shown in the bottom panel of Figure 4, produces a ring with poor contrast between the high and low intensity regions. The primary ring appears weak and there is visible, non-zero intensity within the ring. The second generic axicon, shown in the middle panel, produces a clean ring with a subtly weaker contrast between the edge of the ring and the dark center.
To emphasize the intensity variations within the resulting beams, a false-color scale version of the images was generated and a line profile extracted. Figure 4 shows a side-by-side view of the original (left) and false-colored (right) images; a white line is included to show where the intensity profile was taken from and the corresponding pixel information is shown in Figure 5. A comparison of the line intensities from the three tested axicons shows that the Thorlabs' axicon has the sharpest intensity peaks, i.e. the best contrast, since the intensity goes from bright to dark over the lowest number of pixels. The generic axicons transition from a bright edge to a zero-intensity center over a larger range of pixels, which is visible in the slowly decaying tails of the asymmetric intensity peaks. This results in reduced contrast between the bright ring and hollow center. Please note that the non-zero peak at the center of the ring is an expected feature since only an ideal, perfect axicon will have high intensity edges and zero-intensity everywhere else. By improving the apex rounding diameter and reducing surface imperfections of the axicon, the contrast between the high intensity region and the nonzero center can be improved.
Click to Enlarge
Figure 5: Line profiles extracted from the images of the ring-shaped beams in Figure 4. The Thorlabs axicon produces the sharpest intensity peaks, with the steepest transition from the bright edge to zero-intensity center. Intensity is presented in arbitrary units and is not an absolute measurement. Position is also provided in arbitrary units, but is related to the pixel number.
References
- O. Brzobohatý, T. Cižmár, and P. Zemánek, "High quality quasi-Bessel beam generated by round-tip axicon," Optics Express, Vol. 16, No. 17, pp.12688-12700, 2018.
- B. Dépret, P. Verkerk, and D. Hennequin, "Characterization and modelling of the hollow beam produced by a real conical lens," Optics Communications, Vol. 211, pp. 31-38, 2002.
| Damage Threshold Specifications | ||
|---|---|---|
| Coating Designation (Item # Suffix) |
Damage Threshold | |
| -UV | Pulsed | 5.0 J/cm2 at 355 nm, 10 ns, 10 Hz, Ø0.350 mm |
| -A | Pulsed | 7.5 J/cm2 at 532 nm, 10 ns, 10 Hz, Ø0.491 mm |
| CWa,b | 550 W/cm (532 nm, Ø1.000 mm) | |
| -B | Pulsed | 0.246 J/cm2 at 800 nm, 99 fs, 1 kHz, Ø0.166 mm 7.5 J/cm2 at 810 nm, 10 ns, 10 Hz, Ø0.133 mm |
| CWa,b | 20 kW/cm (1070 nm, Ø0.974 mm) | |
| -C | Pulsed | 7.5 J/cm2 at 1542 nm, 10 ns, 10 Hz, Ø0.189 mm |
| CWa,b | 350 W/cm (1540 nm, Ø1.030 mm) | |
Damage Threshold Data for Thorlabs' UV Fused Silica Axicons
The specifications to the right are measured data for Thorlabs' UV fused silica lenses. Damage threshold specifications are constant for all UV fused silica lenses, regardless of the size of the lens.
Laser Induced Damage Threshold Tutorial
The following is a general overview of how laser induced damage thresholds are measured and how the values may be utilized in determining the appropriateness of an optic for a given application. When choosing optics, it is important to understand the Laser Induced Damage Threshold (LIDT) of the optics being used. The LIDT for an optic greatly depends on the type of laser you are using. Continuous wave (CW) lasers typically cause damage from thermal effects (absorption either in the coating or in the substrate). Pulsed lasers, on the other hand, often strip electrons from the lattice structure of an optic before causing thermal damage. Note that the guideline presented here assumes room temperature operation and optics in new condition (i.e., within scratch-dig spec, surface free of contamination, etc.). Because dust or other particles on the surface of an optic can cause damage at lower thresholds, we recommend keeping surfaces clean and free of debris. For more information on cleaning optics, please see our Optics Cleaning tutorial.
Testing Method
Thorlabs' LIDT testing is done in compliance with ISO/DIS 11254 and ISO 21254 specifications.
First, a low-power/energy beam is directed to the optic under test. The optic is exposed in 10 locations to this laser beam for 30 seconds (CW) or for a number of pulses (pulse repetition frequency specified). After exposure, the optic is examined by a microscope (~100X magnification) for any visible damage. The number of locations that are damaged at a particular power/energy level is recorded. Next, the power/energy is either increased or decreased and the optic is exposed at 10 new locations. This process is repeated until damage is observed. The damage threshold is then assigned to be the highest power/energy that the optic can withstand without causing damage. A histogram such as that below represents the testing of one BB1-E02 mirror.

The photograph above is a protected aluminum-coated mirror after LIDT testing. In this particular test, it handled 0.43 J/cm2 (1064 nm, 10 ns pulse, 10 Hz, Ø1.000 mm) before damage.
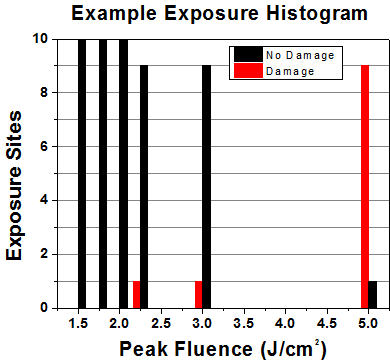
| Example Test Data | |||
|---|---|---|---|
| Fluence | # of Tested Locations | Locations with Damage | Locations Without Damage |
| 1.50 J/cm2 | 10 | 0 | 10 |
| 1.75 J/cm2 | 10 | 0 | 10 |
| 2.00 J/cm2 | 10 | 0 | 10 |
| 2.25 J/cm2 | 10 | 1 | 9 |
| 3.00 J/cm2 | 10 | 1 | 9 |
| 5.00 J/cm2 | 10 | 9 | 1 |
According to the test, the damage threshold of the mirror was 2.00 J/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.803 mm). Please keep in mind that these tests are performed on clean optics, as dirt and contamination can significantly lower the damage threshold of a component. While the test results are only representative of one coating run, Thorlabs specifies damage threshold values that account for coating variances.
Continuous Wave and Long-Pulse Lasers
When an optic is damaged by a continuous wave (CW) laser, it is usually due to the melting of the surface as a result of absorbing the laser's energy or damage to the optical coating (antireflection) [1]. Pulsed lasers with pulse lengths longer than 1 µs can be treated as CW lasers for LIDT discussions.
When pulse lengths are between 1 ns and 1 µs, laser-induced damage can occur either because of absorption or a dielectric breakdown (therefore, a user must check both CW and pulsed LIDT). Absorption is either due to an intrinsic property of the optic or due to surface irregularities; thus LIDT values are only valid for optics meeting or exceeding the surface quality specifications given by a manufacturer. While many optics can handle high power CW lasers, cemented (e.g., achromatic doublets) or highly absorptive (e.g., ND filters) optics tend to have lower CW damage thresholds. These lower thresholds are due to absorption or scattering in the cement or metal coating.
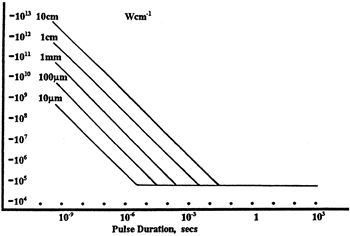
LIDT in linear power density vs. pulse length and spot size. For long pulses to CW, linear power density becomes a constant with spot size. This graph was obtained from [1].
Pulsed lasers with high pulse repetition frequencies (PRF) may behave similarly to CW beams. Unfortunately, this is highly dependent on factors such as absorption and thermal diffusivity, so there is no reliable method for determining when a high PRF laser will damage an optic due to thermal effects. For beams with a high PRF both the average and peak powers must be compared to the equivalent CW power. Additionally, for highly transparent materials, there is little to no drop in the LIDT with increasing PRF.
In order to use the specified CW damage threshold of an optic, it is necessary to know the following:
- Wavelength of your laser
- Beam diameter of your beam (1/e2)
- Approximate intensity profile of your beam (e.g., Gaussian)
- Linear power density of your beam (total power divided by 1/e2 beam diameter)
Thorlabs expresses LIDT for CW lasers as a linear power density measured in W/cm. In this regime, the LIDT given as a linear power density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size, as demonstrated by the graph to the right. Average linear power density can be calculated using the equation below.
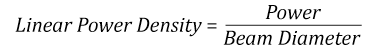
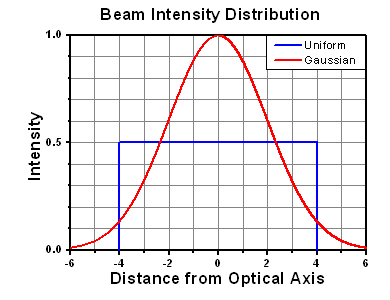
The calculation above assumes a uniform beam intensity profile. You must now consider hotspots in the beam or other non-uniform intensity profiles and roughly calculate a maximum power density. For reference, a Gaussian beam typically has a maximum power density that is twice that of the uniform beam (see lower right).
Now compare the maximum power density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately. A good rule of thumb is that the damage threshold has a linear relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 10 W/cm at 1310 nm scales to 5 W/cm at 655 nm):

While this rule of thumb provides a general trend, it is not a quantitative analysis of LIDT vs wavelength. In CW applications, for instance, damage scales more strongly with absorption in the coating and substrate, which does not necessarily scale well with wavelength. While the above procedure provides a good rule of thumb for LIDT values, please contact Tech Support if your wavelength is different from the specified LIDT wavelength. If your power density is less than the adjusted LIDT of the optic, then the optic should work for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. The damage analysis will be carried out on a similar optic (customer's optic will not be damaged). Testing may result in additional costs or lead times. Contact Tech Support for more information.
Pulsed Lasers
As previously stated, pulsed lasers typically induce a different type of damage to the optic than CW lasers. Pulsed lasers often do not heat the optic enough to damage it; instead, pulsed lasers produce strong electric fields capable of inducing dielectric breakdown in the material. Unfortunately, it can be very difficult to compare the LIDT specification of an optic to your laser. There are multiple regimes in which a pulsed laser can damage an optic and this is based on the laser's pulse length. The highlighted columns in the table below outline the relevant pulse lengths for our specified LIDT values.
Pulses shorter than 10-9 s cannot be compared to our specified LIDT values with much reliability. In this ultra-short-pulse regime various mechanics, such as multiphoton-avalanche ionization, take over as the predominate damage mechanism [2]. In contrast, pulses between 10-7 s and 10-4 s may cause damage to an optic either because of dielectric breakdown or thermal effects. This means that both CW and pulsed damage thresholds must be compared to the laser beam to determine whether the optic is suitable for your application.
| Pulse Duration | t < 10-9 s | 10-9 < t < 10-7 s | 10-7 < t < 10-4 s | t > 10-4 s |
|---|---|---|---|---|
| Damage Mechanism | Avalanche Ionization | Dielectric Breakdown | Dielectric Breakdown or Thermal | Thermal |
| Relevant Damage Specification | No Comparison (See Above) | Pulsed | Pulsed and CW | CW |
When comparing an LIDT specified for a pulsed laser to your laser, it is essential to know the following:
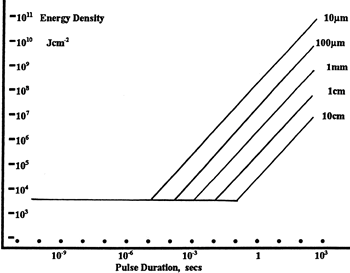
LIDT in energy density vs. pulse length and spot size. For short pulses, energy density becomes a constant with spot size. This graph was obtained from [1].
- Wavelength of your laser
- Energy density of your beam (total energy divided by 1/e2 area)
- Pulse length of your laser
- Pulse repetition frequency (prf) of your laser
- Beam diameter of your laser (1/e2 )
- Approximate intensity profile of your beam (e.g., Gaussian)
The energy density of your beam should be calculated in terms of J/cm2. The graph to the right shows why expressing the LIDT as an energy density provides the best metric for short pulse sources. In this regime, the LIDT given as an energy density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size. This calculation assumes a uniform beam intensity profile. You must now adjust this energy density to account for hotspots or other nonuniform intensity profiles and roughly calculate a maximum energy density. For reference a Gaussian beam typically has a maximum energy density that is twice that of the 1/e2 beam.
Now compare the maximum energy density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately [3]. A good rule of thumb is that the damage threshold has an inverse square root relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 1 J/cm2 at 1064 nm scales to 0.7 J/cm2 at 532 nm):
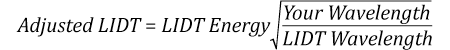
You now have a wavelength-adjusted energy density, which you will use in the following step.
Beam diameter is also important to know when comparing damage thresholds. While the LIDT, when expressed in units of J/cm², scales independently of spot size; large beam sizes are more likely to illuminate a larger number of defects which can lead to greater variances in the LIDT [4]. For data presented here, a <1 mm beam size was used to measure the LIDT. For beams sizes greater than 5 mm, the LIDT (J/cm2) will not scale independently of beam diameter due to the larger size beam exposing more defects.
The pulse length must now be compensated for. The longer the pulse duration, the more energy the optic can handle. For pulse widths between 1 - 100 ns, an approximation is as follows:
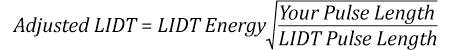
Use this formula to calculate the Adjusted LIDT for an optic based on your pulse length. If your maximum energy density is less than this adjusted LIDT maximum energy density, then the optic should be suitable for your application. Keep in mind that this calculation is only used for pulses between 10-9 s and 10-7 s. For pulses between 10-7 s and 10-4 s, the CW LIDT must also be checked before deeming the optic appropriate for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. Contact Tech Support for more information.
[1] R. M. Wood, Optics and Laser Tech. 29, 517 (1998).
[2] Roger M. Wood, Laser-Induced Damage of Optical Materials (Institute of Physics Publishing, Philadelphia, PA, 2003).
[3] C. W. Carr et al., Phys. Rev. Lett. 91, 127402 (2003).
[4] N. Bloembergen, Appl. Opt. 12, 661 (1973).
In order to illustrate the process of determining whether a given laser system will damage an optic, a number of example calculations of laser induced damage threshold are given below. For assistance with performing similar calculations, we provide a spreadsheet calculator that can be downloaded by clicking the button to the right. To use the calculator, enter the specified LIDT value of the optic under consideration and the relevant parameters of your laser system in the green boxes. The spreadsheet will then calculate a linear power density for CW and pulsed systems, as well as an energy density value for pulsed systems. These values are used to calculate adjusted, scaled LIDT values for the optics based on accepted scaling laws. This calculator assumes a Gaussian beam profile, so a correction factor must be introduced for other beam shapes (uniform, etc.). The LIDT scaling laws are determined from empirical relationships; their accuracy is not guaranteed. Remember that absorption by optics or coatings can significantly reduce LIDT in some spectral regions. These LIDT values are not valid for ultrashort pulses less than one nanosecond in duration.

A Gaussian beam profile has about twice the maximum intensity of a uniform beam profile.
CW Laser Example
Suppose that a CW laser system at 1319 nm produces a 0.5 W Gaussian beam that has a 1/e2 diameter of 10 mm. A naive calculation of the average linear power density of this beam would yield a value of 0.5 W/cm, given by the total power divided by the beam diameter:
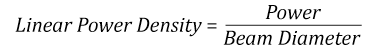
However, the maximum power density of a Gaussian beam is about twice the maximum power density of a uniform beam, as shown in the graph to the right. Therefore, a more accurate determination of the maximum linear power density of the system is 1 W/cm.
An AC127-030-C achromatic doublet lens has a specified CW LIDT of 350 W/cm, as tested at 1550 nm. CW damage threshold values typically scale directly with the wavelength of the laser source, so this yields an adjusted LIDT value:

The adjusted LIDT value of 350 W/cm x (1319 nm / 1550 nm) = 298 W/cm is significantly higher than the calculated maximum linear power density of the laser system, so it would be safe to use this doublet lens for this application.
Pulsed Nanosecond Laser Example: Scaling for Different Pulse Durations
Suppose that a pulsed Nd:YAG laser system is frequency tripled to produce a 10 Hz output, consisting of 2 ns output pulses at 355 nm, each with 1 J of energy, in a Gaussian beam with a 1.9 cm beam diameter (1/e2). The average energy density of each pulse is found by dividing the pulse energy by the beam area:
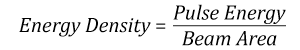
As described above, the maximum energy density of a Gaussian beam is about twice the average energy density. So, the maximum energy density of this beam is ~0.7 J/cm2.
The energy density of the beam can be compared to the LIDT values of 1 J/cm2 and 3.5 J/cm2 for a BB1-E01 broadband dielectric mirror and an NB1-K08 Nd:YAG laser line mirror, respectively. Both of these LIDT values, while measured at 355 nm, were determined with a 10 ns pulsed laser at 10 Hz. Therefore, an adjustment must be applied for the shorter pulse duration of the system under consideration. As described on the previous tab, LIDT values in the nanosecond pulse regime scale with the square root of the laser pulse duration:
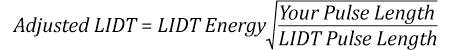
This adjustment factor results in LIDT values of 0.45 J/cm2 for the BB1-E01 broadband mirror and 1.6 J/cm2 for the Nd:YAG laser line mirror, which are to be compared with the 0.7 J/cm2 maximum energy density of the beam. While the broadband mirror would likely be damaged by the laser, the more specialized laser line mirror is appropriate for use with this system.
Pulsed Nanosecond Laser Example: Scaling for Different Wavelengths
Suppose that a pulsed laser system emits 10 ns pulses at 2.5 Hz, each with 100 mJ of energy at 1064 nm in a 16 mm diameter beam (1/e2) that must be attenuated with a neutral density filter. For a Gaussian output, these specifications result in a maximum energy density of 0.1 J/cm2. The damage threshold of an NDUV10A Ø25 mm, OD 1.0, reflective neutral density filter is 0.05 J/cm2 for 10 ns pulses at 355 nm, while the damage threshold of the similar NE10A absorptive filter is 10 J/cm2 for 10 ns pulses at 532 nm. As described on the previous tab, the LIDT value of an optic scales with the square root of the wavelength in the nanosecond pulse regime:
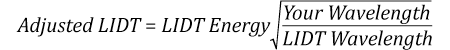
This scaling gives adjusted LIDT values of 0.08 J/cm2 for the reflective filter and 14 J/cm2 for the absorptive filter. In this case, the absorptive filter is the best choice in order to avoid optical damage.
Pulsed Microsecond Laser Example
Consider a laser system that produces 1 µs pulses, each containing 150 µJ of energy at a repetition rate of 50 kHz, resulting in a relatively high duty cycle of 5%. This system falls somewhere between the regimes of CW and pulsed laser induced damage, and could potentially damage an optic by mechanisms associated with either regime. As a result, both CW and pulsed LIDT values must be compared to the properties of the laser system to ensure safe operation.
If this relatively long-pulse laser emits a Gaussian 12.7 mm diameter beam (1/e2) at 980 nm, then the resulting output has a linear power density of 5.9 W/cm and an energy density of 1.2 x 10-4 J/cm2 per pulse. This can be compared to the LIDT values for a WPQ10E-980 polymer zero-order quarter-wave plate, which are 5 W/cm for CW radiation at 810 nm and 5 J/cm2 for a 10 ns pulse at 810 nm. As before, the CW LIDT of the optic scales linearly with the laser wavelength, resulting in an adjusted CW value of 6 W/cm at 980 nm. On the other hand, the pulsed LIDT scales with the square root of the laser wavelength and the square root of the pulse duration, resulting in an adjusted value of 55 J/cm2 for a 1 µs pulse at 980 nm. The pulsed LIDT of the optic is significantly greater than the energy density of the laser pulse, so individual pulses will not damage the wave plate. However, the large average linear power density of the laser system may cause thermal damage to the optic, much like a high-power CW beam.
| Posted Comments: | |
user
(posted 2023-04-18 09:04:03.437) Good morning.
I want to try one of your axicons to turn the 1064 or 532 nm gaussian output beam (approx. 7 mm in diameter) of a pulsed Nd:YAG laser into a ring. Such ring will be additionally expanding and refocussed. Some colleagues have warn me that the axicon itself will focussed the laser beam. I am not happy with that, as my beam will be at least 70 mJ/pulse.
Could you please let me know if your axicons will focussed my the axicon, of if there is any consideration I should take to avoid this effect?
Thanks in advance.
Jose M. Vadillo cdolbashian
(posted 2023-04-26 09:56:47.0) Thank you for reaching out to you with this inquiry! Unfortunately for both this device and the vortex wave plate (which can create a donut-like intensity profile), the beam will pass through a tight focus, either at the lens surface or at a focal point beyond it. Perhaps you would have some luck using a multimode fiber and modifying the launch conditions to generate a donut-like output. user
(posted 2022-10-27 23:48:31.58) As you know, researchers always use a axicon or SLM to generate Bessel beam and use a Fourier lens(L1) to transform it into a ring. In most cases, there is always a 4f set up, consisting of two lenses with the same focal length(L2、L3), which transmits the ring to the back focal plane of the objective. Recently I tried the set up and found the ring in the focal plane of L1. However, I can't find Bessel beam in the focal plane of L2. To my surprise, when I move back the CCD, I found the Bessel beam in the plane twice focal length away L2. I want to consult you whether you have met the same situation. I would sincerely appreciate you if you can reply to this question. ksosnowski
(posted 2022-11-11 05:03:12.0) Hello, thanks for reaching out to Thorlabs. This seems to be a mixup with the conjugate planes of your system. I have reached out directly to discuss this further. Hung Wei Liu
(posted 2022-10-20 18:02:09.63) Hello, I have a question about the different physical angle of axicon. I want to know the disadvantage about the small physical angle of axicon. cdolbashian
(posted 2022-10-24 09:36:09.0) Thank you for reaching out to us with this inquiry. I have reached out to you directly to discuss this more. The small physical angle increases the depth of focus and decreases the divergence angle for the generated Bessel ring. seongjun park
(posted 2022-08-17 11:31:17.473) I am wondering the edge thickness and center thickness tolerances are both ranging from +0.1/-0.0 mm, not +0.1/-0.1. cdolbashian
(posted 2022-09-07 02:38:45.0) Thank you for your inquiry regarding our tolerancing. The asymmetric tolerances are simply due to our machining process. 18840853650
(posted 2017-09-08 10:09:15.43) 你好,
我购买了一款AX255-C的锥透镜,想仿真一下1310nm和527nm激光通过该锥透镜后的光斑发布效果,即贝塞尔光发布情况,但是你们给的ZEMAX文件版本太高我用不了,所以想咨询一下你们可以帮我仿真一下这个效果嘛?
非常感谢,期待您的回信。 tfrisch
(posted 2017-09-15 01:16:54.0) Hello, thank you for contacting Thorlabs. I will have a representative from our office in China reach out to you about an appropriate format for this optical model. daniel.comparat
(posted 2016-04-12 13:57:18.56) We found that the center is not precisely machined. For small diameter initial beams (1 mm) the axcicon is more like a lens.
I send you an e-mail to the tehnical department to have more news, but I did not received any answer.
Could you try to contact them.
Best
Daniel Comparat besembeson
(posted 2016-04-13 09:57:52.0) Response from Bweh at Thorlabs USA: We contacted you yesterday to get more details about your application and observations, which may be related to the precision level of the apex rounding of our axicons. andreas.boenke
(posted 2016-01-19 14:21:19.817) Dear Sirs,
can you please provide information about the max. radius of the axicon tip area with significant deviation from the theoretical shape (causing aberrated beam portion) ?
This would be interesting for
AX2510-A
AX255-A
AX252-A
Thank you for your help.
Best regards,
Andreas Boenke besembeson
(posted 2016-01-21 11:17:59.0) Response from Bweh at Thorlabs USA: I will be contacting you with this information. user
(posted 2015-11-19 13:23:45.527) A tutorial, or some other explanation (ABCD matrix for example) on axicons in the prism guide would be helpful. myanakas
(posted 2015-11-19 09:05:51.0) Response from Mike at Thorlabs: Thank you for your feedback. We will look into adding this information to our Prism Guide in the future. dennis-weller
(posted 2013-07-02 11:50:34.36) Can you please send me Zemax-Files of you axicon lenses?
Thanks in anticipation! cdaly
(posted 2013-07-09 09:29:00.0) Thank you for your feedback. We've just updated the webpage to include these files now. tcohen
(posted 2013-01-03 15:07:00.0) Response from Tim at Thorlabs: The rings could be a result from imperfections in the tip of the axicon, however, the quality of the tip of these optics are unrivaled in the industry and would make this an unlikely reason. Misalignment could contribute. Possibly you are seeing artifacts of the Bessel beam that is generated when a Gaussian beam is inputted. This is touched upon under the “Beam Shape tab on this page. We will work to improve the discussion on this page to better explain the performance of these parts and options you may have to achieve desirable results. We will contact you to troubleshoot this artifact in your setup. totlab
(posted 2012-12-11 23:05:54.373) We bought a axicon and found the ring is not so clean, and several smaller rings are in the inner side. The laser beam is collimated and dia=2mm.
Is it because the imperfection of the tip of the axicon? I found no dust or damage on the surface. jjurado
(posted 2011-02-04 10:57:00.0) Response from Javier at Thorlabs to info: Thank you very much for contacting us with your inquiry. Since axicons produce a ring-shaped beam, they work well for replacing the dark field patch stop in a dark field microscope. Although we have not yet developed an application in dark field microscopy using axicons, there have been several publications in this field. You can find one of these publications through the following link: http://spiedigitallibrary.org/jbo/resource/1/jbopfo/v13/i4/p044024_s1?isAuthorized=no info
(posted 2011-02-03 14:54:44.0) Would this be a good lens to use in a the light source path of a dark field microscope? |
Selection Guide for Prisms
Thorlabs offers a wide variety of prisms, which can be used to reflect, invert, rotate, disperse, steer, and collimate light. For prisms and substrates not listed below, please contact Tech Support.
Beam Steering Prisms
| Prism | Material | Deviation | Invert | Reverse or Rotate | Illustration | Applications |
|---|---|---|---|---|---|---|
| Right Angle Prisms | N-BK7, UV Fused Silica, Calcium Fluoride, or Zinc Selenide | 90° | 90° | No | 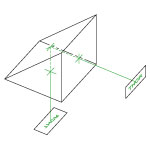 |
90° reflector used in optical systems such as telescopes and periscopes. |
| 180° | 180° | No | 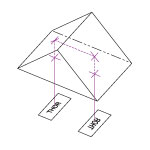 |
180° reflector, independent of entrance beam angle. Acts as a non-reversing mirror and can be used in binocular configurations. |
||
| TIR Retroreflectors (Unmounted and Mounted) and Specular Retroreflectors (Unmounted and Mounted) |
N-BK7 | 180° | 180° | No | 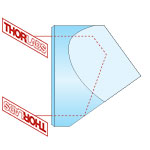 |
180° reflector, independent of entrance beam angle. Beam alignment and beam delivery. Substitute for mirror in applications where orientation is difficult to control. |
| Unmounted Penta Prisms and Mounted Penta Prisms |
N-BK7 | 90° | No | No | 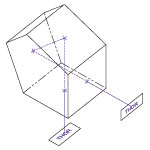 |
90° reflector, without inversion or reversal of the beam profile. Can be used for alignment and optical tooling. |
| Roof Prisms | N-BK7 | 90° | 90° | 180o Rotation | 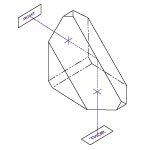 |
90° reflector, inverted and rotated (deflected left to right and top to bottom). Can be used for alignment and optical tooling. |
| Unmounted Dove Prisms and Mounted Dove Prisms |
N-BK7 | No | 180° | 2x Prism Rotation | 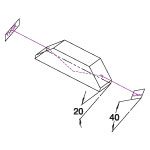 |
Dove prisms may invert, reverse, or rotate an image based on which face the light is incident on. Prism in a beam rotator orientation. |
| 180° | 180° | No | 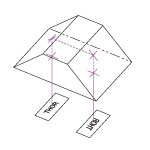 |
Prism acts as a non-reversing mirror. Same properties as a retroreflector or right angle (180° orientation) prism in an optical setup. |
||
| Wedge Prisms | N-BK7 | Models Available from 2° to 10° | No | No | 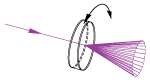 |
Beam steering applications. By rotating one wedged prism, light can be steered to trace the circle defined by 2 times the specified deviation angle. |
| No | No | 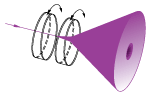 |
Variable beam steering applications. When both wedges are rotated, the beam can be moved anywhere within the circle defined by 4 times the specified deviation angle. |
|||
| Coupling Prisms | Rutile (TiO2) or GGG | Variablea | No | No | 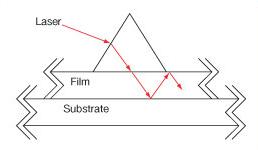 |
High index of refraction substrate used to couple light into films. Rutile used for nfilm > 1.8 GGG used for nfilm < 1.8 |
Dispersive Prisms
| Prism | Material | Deviation | Invert | Reverse or Rotate | Illustration | Applications |
|---|---|---|---|---|---|---|
| Equilateral Prisms | F2, N-F2, N-SF11, Calcium Fluoride, or Zinc Selenide |
Variablea | No | No | 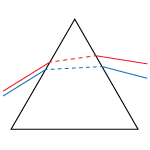 |
Dispersion prisms are a substitute for diffraction gratings. Use to separate white light into visible spectrum. |
| Dispersion Compensating Prism Pairs | Fused Silica, Calcium Fluoride, SF10, or N-SF14 | Variable Vertical Offset | No | No | 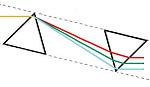 |
Compensate for pulse broadening effects in ultrafast laser systems. Can be used as an optical filter, for wavelength tuning, or dispersion compensation.
|
| Pellin Broca Prisms | N-BK7, UV Fused Silica, or Calcium Fluoride |
90° | 90° | No | 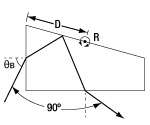 |
Ideal for wavelength separation of a beam of light, output at 90°. Used to separate harmonics of a laser or compensate for group velocity dispersion. |
Beam Manipulating Prisms
| Prism | Material | Deviation | Invert | Reverse or Rotate | Illustration | Applications |
|---|---|---|---|---|---|---|
| Anamorphic Prism Pairs | N-KZFS8 or N-SF11 |
Variable Vertical Offset | No | No | 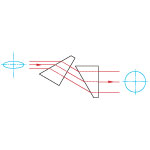 |
Variable magnification along one axis. Collimating elliptical beams (e.g., laser diodes) Converts an elliptical beam into a circular beam by magnifying or contracting the input beam in one axis. |
| Axicons (UVFS, ZnSe) | UV Fused Silica or Zinc Selenide |
Variablea | No | No |
Creates a conical, non-diverging beam with a Bessel intensity profile from a collimated source. |
Polarization Altering Prisms
| Prism | Material | Deviation | Invert | Reverse or Rotate | Illustration | Applications |
|---|---|---|---|---|---|---|
| Glan-Taylor, Glan-Laser, and α-BBO Glan-Laser Polarizers | Glan-Taylor: Calcite Glan-Laser: α-BBO or Calcite |
p-pol. - 0° s-pol. - 112°a |
No | No | 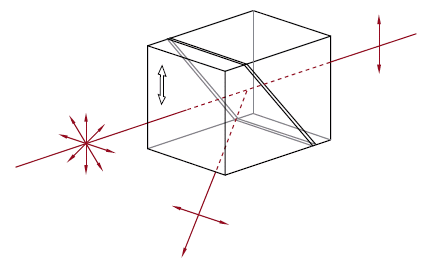 |
Double prism configuration and birefringent calcite produce extremely pure linearly polarized light. Total Internal Reflection of s-pol. at the gap between the prism while p-pol. is transmitted. |
| Rutile Polarizers | Rutile (TiO2) | s-pol. - 0° p-pol. absorbed by housing |
No | No | 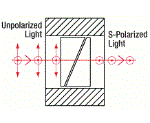 |
Double prism configuration and birefringent rutile (TiO2) produce extremely pure linearly polarized light. Total Internal Reflection of p-pol. at the gap between the prisms while s-pol. is transmitted.
|
| Double Glan-Taylor Polarizers | Calcite | p-pol. - 0° s-pol. absorbed by housing |
No | No |  |
Triple prism configuration and birefringent calcite produce maximum polarized field over a large half angle. Total Internal Reflection of s-pol. at the gap between the prism while p-pol. is transmitted. |
| Glan Thompson Polarizers | Calcite | p-pol. - 0° s-pol. absorbed by housing |
No | No | 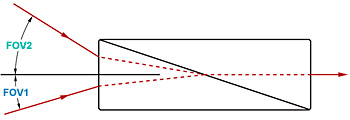 |
Double prism configuration and birefringent calcite produce a polarizer with the widest field of view while maintaining a high extinction ratio. Total Internal Reflection of s-pol. at the gap between the prism while p-pol. is transmitted. |
| Wollaston Prisms and Wollaston Polarizers |
Quartz, Magnesium Fluoride, α-BBO, Calcite, Yttrium Orthovanadate | Symmetric p-pol. and s-pol. deviation angle |
No | No | 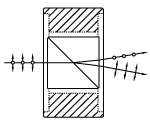 |
Double prism configuration and birefringent calcite produce the widest deviation angle of beam displacing polarizers. s-pol. and p-pol. deviate symmetrically from the prism. Wollaston prisms are used in spectrometers and polarization analyzers. |
| Rochon Prisms | Magnesium Fluoride or Yttrium Orthovanadate |
Ordinary Ray: 0° Extraordinary Ray: deviation angle |
No | No | 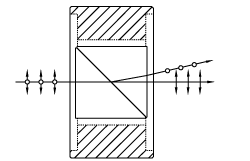 |
Double prism configuration and birefringent MgF2 or YVO4 produce a small deviation angle with a high extinction ratio. Extraordinary ray deviates from the input beam's optical axis, while ordinary ray does not deviate. |
| Beam Displacing Prisms | Calcite | 2.7 or 4.0 mm Beam Displacement | No | No | 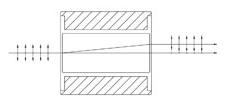 |
Single prism configuration and birefringent calcite separate an input beam into two orthogonally polarized output beams. s-pol. and p-pol. are displaced by 2.7 or 4.0 mm. Beam displacing prisms can be used as polarizing beamsplitters where 90o separation is not possible. |
| Fresnel Rhomb Retarders | N-BK7 | Linear to circular polarization Vertical Offset |
No | No | 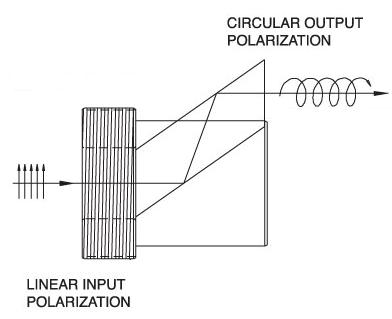 |
λ/4 Fresnel Rhomb Retarder turns a linear input into circularly polarized output. Uniform λ/4 retardance over a wider wavelength range compared to birefringent wave plates. |
| Rotates linearly polarized light 90° | No | No | 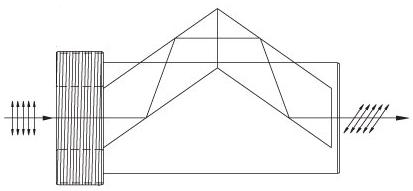 |
λ/2 Fresnel Rhomb Retarder rotates linearly polarized light 90°. Uniform λ/2 retardance over a wider wavelength range compared to birefringent wave plates. |
Beamsplitter Prisms
| Prism | Material | Deviation | Invert | Reverse or Rotate | Illustration | Applications |
|---|---|---|---|---|---|---|
| Beamsplitter Cubes | N-BK7 | 50:50 splitting ratio, 0° and 90° s- and p- pol. within 10% of each other |
No | No | 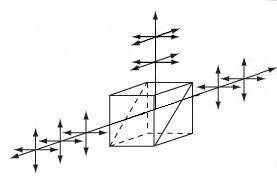 |
Double prism configuration and dielectric coating provide 50:50 beamsplitting nearly independent of polarization. Non-polarizing beamsplitter over the specified wavelength range. |
| Polarizing Beamsplitter Cubes | N-BK7, UV Fused Silica, or N-SF1 | p-pol. - 0° s-pol. - 90° |
No | No | 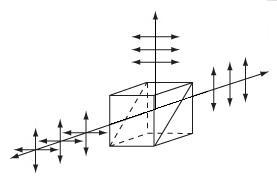 |
Double prism configuration and dielectric coating transmit p-pol. light and reflect s-pol. light. For highest polarization use the transmitted beam. |

These axicons are uncoated and operate in the 185 nm - 2.1 µm wavelength range. The substrate used for these lenses, UV fused silica, is an ideal choice for applications from the UV to the near IR. UV fused silica has better homogeneity and a lower coefficient of thermal expansion than N-BK7.

This axicon is AR coated for the 245 - 400 nm range. It is designed to offer high transmission in the UV range, making it ideal for many ultraviolet applications. Furthermore, the substrate being used, UV fused silica, offers excellent UV transmission.
| Item # | Diameter | Physical Angle (α) | Deflection Angle (β)a | Center Thickness (tc) |
AR Coatingb | AR Coating Plotb |
Reference Drawing |
|---|---|---|---|---|---|---|---|
| AX251-UV | Ø1" (Ø25.4 mm) |
1.0° | 0.5° | 5.2 mm | 245 - 400 nm Ravg<0.5% |
Raw Data |

These axicons are AR coated for the 350 - 700 nm range. They are well-suited for applications within part of the near UV (NUV) spectrum and all of the visible spectrum. This range makes these axicons ideal for use with HeNe and other visible lasers.

These axicons are AR coated for the 650-1050 nm range making them suitable for many near IR (NIR) applications, such as optical traps and corneal surgeries.

These axicons are AR coated for the 1050 - 1700 nm range, which makes them great for applications into the near IR (NIR). This covers common wavelengths used in applications such as: optical coherence tomography (OCT), optical trapping, and laser drilling. In these applications, an axicon can increase the depth of focus in the sample arm.
 Products Home
Products Home











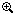 Zoom
Zoom



 UV Fused Silica Axicons, Unmounted
UV Fused Silica Axicons, Unmounted