Hastings Triplet Achromatic Lenses
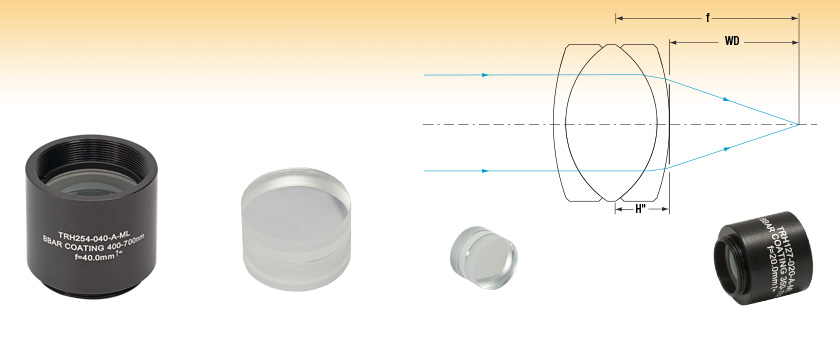
- Optimized for Infinite Conjugate Ratios
- AR Coating: 400 - 700 nm
- Good On-Axis and Off-Axis Performance
- Ideal for Compensation of Lateral and
Axial Chromatic Aberrations
TRH254-040-A-ML
SM1-Threaded Housing
TRH254-040-A
Ø1" Unmounted
TRH064-010-A
Ø1/4" Unmounted
TRH127-020-A-ML
SM05-Threaded Housing

Please Wait
| Common Specifications | |
|---|---|
| Design Wavelengths | 486.1 nm, 587.6 nm, 656.3 nm |
| Clear Aperture | >90% of Lens Diameter |
| Lens Diameter Tolerance | +0.00/-0.10 mm |
| Focal Length Tolerance | ±1% |
| Surface Quality | 40-20 Scratch-Dig |
| Centration | <3 arcmin |
| AR Coating Range | 400 - 700 nm |
| Average Reflectancea | <0.5% |
| Damage Thresholdb | 30 MW/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.566 mm) |
| Operating Temperature | -40 to 85 oC |
| Click on the red Document icon next to the item numbers below to access the Zemax file download. For the mounted triplets, refer to the files for the corresponding unmounted triplets. |
Features
- Mounted and Unmounted Hastings Achromatic Triplets
- Ø1/4", Ø1/2", and Ø1" Unmounted Versions
- SM05- or SM1-Threaded Mounted Versions
- AR Coated for the 400 - 700 nm Range (Ravg <0.5%)
- Excellent Aberration Compensation
Thorlabs' Hastings achromatic triplets are designed to provide an infinite conjugate ratio and are useful for focusing collimated beams and for magnification. An achromatic triplet is the simplest lens that corrects for all primary chromatic aberrations. These triplets consist of a low-index center element cemented between two identical high-index outer elements (see the tables below for more information) and feature good on-axis and off-axis performance. For triplets that provide a finite conjugate ratio and 1:1 imaging, please see our Steinheil triplets.
Our Hastings triplets are available unmounted or mounted. Our unmounted triplets are available in Ø1/4", Ø1/2", or Ø1" sizes. Our Ø1/2" and Ø1" mounted triplets feature SM05 (0.535"-40) and SM1 (1.035"-40) threading, respectively, along with a laser engraving of the item #, coating range, and focal length.
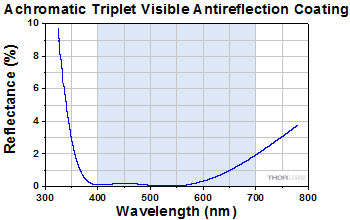
Click to Enlarge
This theoretical graph shows the percent reflectance of the AR coating as a function of wavelength. The shading indicates the region for which the AR coating is optimized. Performance outside of that range is not guaranteed.
| Damage Threshold Specifications | |
|---|---|
| Damage Specification Type | Damage Threshold |
| Pulse | 30 MW/cm2 (532 nm, 10 ns, 10 Hz, Ø0.566 mm) |
Damage Threshold Data for Thorlabs' Visible Achromatic Triplets
The specifications to the right are measured data for Thorlabs' visible achromatic triplets. Damage threshold specifications are constant for all visible achromatic triplets, regardless of the size or the focal length of the achromatic triplet.
Laser Induced Damage Threshold Tutorial
The following is a general overview of how laser induced damage thresholds are measured and how the values may be utilized in determining the appropriateness of an optic for a given application. When choosing optics, it is important to understand the Laser Induced Damage Threshold (LIDT) of the optics being used. The LIDT for an optic greatly depends on the type of laser you are using. Continuous wave (CW) lasers typically cause damage from thermal effects (absorption either in the coating or in the substrate). Pulsed lasers, on the other hand, often strip electrons from the lattice structure of an optic before causing thermal damage. Note that the guideline presented here assumes room temperature operation and optics in new condition (i.e., within scratch-dig spec, surface free of contamination, etc.). Because dust or other particles on the surface of an optic can cause damage at lower thresholds, we recommend keeping surfaces clean and free of debris. For more information on cleaning optics, please see our Optics Cleaning tutorial.
Testing Method
Thorlabs' LIDT testing is done in compliance with ISO/DIS 11254 and ISO 21254 specifications.
First, a low-power/energy beam is directed to the optic under test. The optic is exposed in 10 locations to this laser beam for 30 seconds (CW) or for a number of pulses (pulse repetition frequency specified). After exposure, the optic is examined by a microscope (~100X magnification) for any visible damage. The number of locations that are damaged at a particular power/energy level is recorded. Next, the power/energy is either increased or decreased and the optic is exposed at 10 new locations. This process is repeated until damage is observed. The damage threshold is then assigned to be the highest power/energy that the optic can withstand without causing damage. A histogram such as that below represents the testing of one BB1-E02 mirror.

The photograph above is a protected aluminum-coated mirror after LIDT testing. In this particular test, it handled 0.43 J/cm2 (1064 nm, 10 ns pulse, 10 Hz, Ø1.000 mm) before damage.
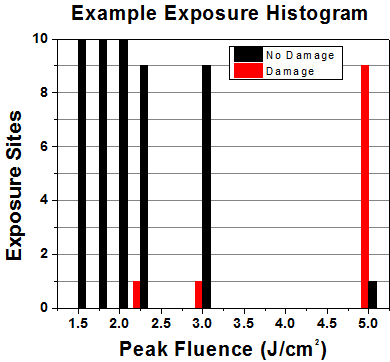
| Example Test Data | |||
|---|---|---|---|
| Fluence | # of Tested Locations | Locations with Damage | Locations Without Damage |
| 1.50 J/cm2 | 10 | 0 | 10 |
| 1.75 J/cm2 | 10 | 0 | 10 |
| 2.00 J/cm2 | 10 | 0 | 10 |
| 2.25 J/cm2 | 10 | 1 | 9 |
| 3.00 J/cm2 | 10 | 1 | 9 |
| 5.00 J/cm2 | 10 | 9 | 1 |
According to the test, the damage threshold of the mirror was 2.00 J/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.803 mm). Please keep in mind that these tests are performed on clean optics, as dirt and contamination can significantly lower the damage threshold of a component. While the test results are only representative of one coating run, Thorlabs specifies damage threshold values that account for coating variances.
Continuous Wave and Long-Pulse Lasers
When an optic is damaged by a continuous wave (CW) laser, it is usually due to the melting of the surface as a result of absorbing the laser's energy or damage to the optical coating (antireflection) [1]. Pulsed lasers with pulse lengths longer than 1 µs can be treated as CW lasers for LIDT discussions.
When pulse lengths are between 1 ns and 1 µs, laser-induced damage can occur either because of absorption or a dielectric breakdown (therefore, a user must check both CW and pulsed LIDT). Absorption is either due to an intrinsic property of the optic or due to surface irregularities; thus LIDT values are only valid for optics meeting or exceeding the surface quality specifications given by a manufacturer. While many optics can handle high power CW lasers, cemented (e.g., achromatic doublets) or highly absorptive (e.g., ND filters) optics tend to have lower CW damage thresholds. These lower thresholds are due to absorption or scattering in the cement or metal coating.
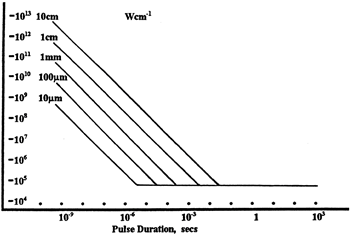
LIDT in linear power density vs. pulse length and spot size. For long pulses to CW, linear power density becomes a constant with spot size. This graph was obtained from [1].
Pulsed lasers with high pulse repetition frequencies (PRF) may behave similarly to CW beams. Unfortunately, this is highly dependent on factors such as absorption and thermal diffusivity, so there is no reliable method for determining when a high PRF laser will damage an optic due to thermal effects. For beams with a high PRF both the average and peak powers must be compared to the equivalent CW power. Additionally, for highly transparent materials, there is little to no drop in the LIDT with increasing PRF.
In order to use the specified CW damage threshold of an optic, it is necessary to know the following:
- Wavelength of your laser
- Beam diameter of your beam (1/e2)
- Approximate intensity profile of your beam (e.g., Gaussian)
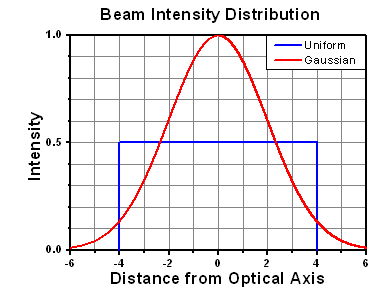
- Linear power density of your beam (total power divided by 1/e2 beam diameter)
Thorlabs expresses LIDT for CW lasers as a linear power density measured in W/cm. In this regime, the LIDT given as a linear power density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size, as demonstrated by the graph to the right. Average linear power density can be calculated using the equation below.
The calculation above assumes a uniform beam intensity profile. You must now consider hotspots in the beam or other non-uniform intensity profiles and roughly calculate a maximum power density. For reference, a Gaussian beam typically has a maximum power density that is twice that of the uniform beam (see lower right).
Now compare the maximum power density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately. A good rule of thumb is that the damage threshold has a linear relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 10 W/cm at 1310 nm scales to 5 W/cm at 655 nm):

While this rule of thumb provides a general trend, it is not a quantitative analysis of LIDT vs wavelength. In CW applications, for instance, damage scales more strongly with absorption in the coating and substrate, which does not necessarily scale well with wavelength. While the above procedure provides a good rule of thumb for LIDT values, please contact Tech Support if your wavelength is different from the specified LIDT wavelength. If your power density is less than the adjusted LIDT of the optic, then the optic should work for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. The damage analysis will be carried out on a similar optic (customer's optic will not be damaged). Testing may result in additional costs or lead times. Contact Tech Support for more information.
Pulsed Lasers
As previously stated, pulsed lasers typically induce a different type of damage to the optic than CW lasers. Pulsed lasers often do not heat the optic enough to damage it; instead, pulsed lasers produce strong electric fields capable of inducing dielectric breakdown in the material. Unfortunately, it can be very difficult to compare the LIDT specification of an optic to your laser. There are multiple regimes in which a pulsed laser can damage an optic and this is based on the laser's pulse length. The highlighted columns in the table below outline the relevant pulse lengths for our specified LIDT values.
Pulses shorter than 10-9 s cannot be compared to our specified LIDT values with much reliability. In this ultra-short-pulse regime various mechanics, such as multiphoton-avalanche ionization, take over as the predominate damage mechanism [2]. In contrast, pulses between 10-7 s and 10-4 s may cause damage to an optic either because of dielectric breakdown or thermal effects. This means that both CW and pulsed damage thresholds must be compared to the laser beam to determine whether the optic is suitable for your application.
| Pulse Duration | t < 10-9 s | 10-9 < t < 10-7 s | 10-7 < t < 10-4 s | t > 10-4 s |
|---|---|---|---|---|
| Damage Mechanism | Avalanche Ionization | Dielectric Breakdown | Dielectric Breakdown or Thermal | Thermal |
| Relevant Damage Specification | No Comparison (See Above) | Pulsed | Pulsed and CW | CW |
When comparing an LIDT specified for a pulsed laser to your laser, it is essential to know the following:
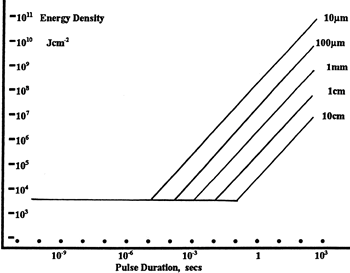
LIDT in energy density vs. pulse length and spot size. For short pulses, energy density becomes a constant with spot size. This graph was obtained from [1].
- Wavelength of your laser
- Energy density of your beam (total energy divided by 1/e2 area)
- Pulse length of your laser
- Pulse repetition frequency (prf) of your laser
- Beam diameter of your laser (1/e2 )
- Approximate intensity profile of your beam (e.g., Gaussian)
The energy density of your beam should be calculated in terms of J/cm2. The graph to the right shows why expressing the LIDT as an energy density provides the best metric for short pulse sources. In this regime, the LIDT given as an energy density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size. This calculation assumes a uniform beam intensity profile. You must now adjust this energy density to account for hotspots or other nonuniform intensity profiles and roughly calculate a maximum energy density. For reference a Gaussian beam typically has a maximum energy density that is twice that of the 1/e2 beam.
Now compare the maximum energy density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately [3]. A good rule of thumb is that the damage threshold has an inverse square root relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 1 J/cm2 at 1064 nm scales to 0.7 J/cm2 at 532 nm):
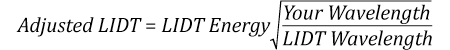
You now have a wavelength-adjusted energy density, which you will use in the following step.
Beam diameter is also important to know when comparing damage thresholds. While the LIDT, when expressed in units of J/cm², scales independently of spot size; large beam sizes are more likely to illuminate a larger number of defects which can lead to greater variances in the LIDT [4]. For data presented here, a <1 mm beam size was used to measure the LIDT. For beams sizes greater than 5 mm, the LIDT (J/cm2) will not scale independently of beam diameter due to the larger size beam exposing more defects.
The pulse length must now be compensated for. The longer the pulse duration, the more energy the optic can handle. For pulse widths between 1 - 100 ns, an approximation is as follows:
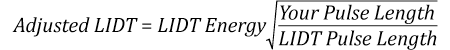
Use this formula to calculate the Adjusted LIDT for an optic based on your pulse length. If your maximum energy density is less than this adjusted LIDT maximum energy density, then the optic should be suitable for your application. Keep in mind that this calculation is only used for pulses between 10-9 s and 10-7 s. For pulses between 10-7 s and 10-4 s, the CW LIDT must also be checked before deeming the optic appropriate for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. Contact Tech Support for more information.
[1] R. M. Wood, Optics and Laser Tech. 29, 517 (1998).
[2] Roger M. Wood, Laser-Induced Damage of Optical Materials (Institute of Physics Publishing, Philadelphia, PA, 2003).
[3] C. W. Carr et al., Phys. Rev. Lett. 91, 127402 (2003).
[4] N. Bloembergen, Appl. Opt. 12, 661 (1973).
| Posted Comments: | |
ILIYA SHOFMAN
(posted 2024-09-28 00:28:50.487) Is the curve of focal length versus wavelength (chromatic focal shift) available for these achromatic triplet lenses? blarowe
(posted 2024-10-09 03:35:14.0) Thank you for reaching out to us. Focal shift curves can be obtained by clicking on the "Graphs" icon in the specs table. Hitesh Mamgain
(posted 2022-11-14 04:22:45.823) Do you have Achromat Triplets for 750nm to 1500nm range i.e. the B series of optics that are available in Achromat Doublets? Luciano Olivo
(posted 2021-04-21 12:34:28.66) The *.zar files that you provide cannot be imported in Optalix LT (as is instead easily possible with *.zmx files).
Please, can you provide also *.otx (or plain *.zmx) files in your downloadable documentation?
Currently it would be useful for me to get the *.zmx files for two cemented triplets, TRH254-040-A and TRS254-040-A, to compare their performance in an intermediate condition between infinite-conjugate ratio and 1:1 finite conjugate, to choose the best one.
Luciano YLohia
(posted 2021-04-21 03:10:43.0) Hello Luciano, thank you for contacting Thorlabs. I have reached out to you directly with the .zmx files for these two parts. akuznetsov
(posted 2018-10-03 17:49:11.083) Can you please provide a comparison between "NIR Air-Spaced Achromatic Doublets" and "Hastings Triplet Achromatic Lenses", not sure I understand the difference? nbayconich
(posted 2018-10-22 08:44:28.0) Thank you for contacting Thorlabs. The Hasting's triplets will have better achromatic performance as well as front to back symmetry to help control coma and astigmatism. When compared to cemented doublets, the triplets will have better performance off axis.
Our air spaced doublets can have better performance than the hastings triplet in terms of controlling spherical aberrations. Aberrations for the air spaced doublets are dominated by astigmatism, distortion, and some higher order coma. In the triplet design, spherical aberration is still the dominant source of error. francois.parnet
(posted 2015-11-24 13:49:52.413) Hi,
Is the triplet achromatic lens can be used to collimate a beam by simply reversing it?
Best regards,
Francois besembeson
(posted 2015-12-02 12:41:38.0) Response from Bweh at Thorlabs USA: Yes the lens assembly is symmetrical and can be used in either direction for collimation from a point source. |


 Products Home
Products Home













 Hastings Achromatic Triplets
Hastings Achromatic Triplets