
Wedged Plate Beamsplitter

- Uncoated UV Fused Silica Beamsplitter
- 5° Wedge Angle Separates Multiple Reflections
- Rectangular Shape Simplifies Mounting
BSF2550
BSF2550 Mounted in a KM100C
Rectangular Optic Mount
OVERVIEW
Features
- Uncoated, Wedged Surface Creates Separated Attenuated Copies of an Incident Beam
- Ideal for High-Power Beam Attenuation
- Multiple Outputs may be Utilized for Different Experiments or Beam Monitoring
Thorlabs' Wedged Optical Beamsplitter is designed to separate a single input beam into multiple copies through successive reflections and refractions, as shown in the figure to the right. It is manufactured from UV fused silica, which offers transmission over the broad wavelength range from 185 nm to 2.1 µm. The wedge is formed using a 5° apex angle, which is designed to provide good separation between the multiple outputs. The rectangular shape allows for precise positioning of the output beams in a plane. It is 1" tall, ideal for mounting in our kinematic rectangular optic mounts or our fixed rectangular optic mount. The wedge is parallel to a 2" long surface, which allows for numerous copy beams to be created.
Upon each reflection and refraction, some of the input power will be lost; hence, the wedged beamsplitter may be used as an attenuator. Since the wedge is uncoated, the power handling will be increased above that for our neutral density filters. Successive transmitted or reflected beams might also be used for different experiments or multiple methods of beam monitoring, such as monitoring power fluctuations using a power meter or other detector, such as a camera or photodiode. Unused output beams can be blocked using a beam dump.
The angular deviation of the output beams may be easily calculated. For details, please see the Theory tab above. For more details on the theory of operation, please see the reference at the end of the Theory tab.
SPECS
Click to Enlarge
Click Here for Raw Data
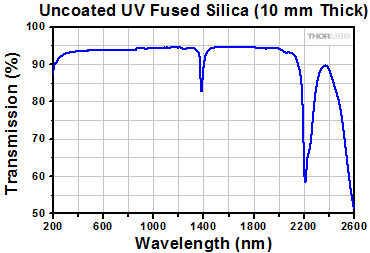
Plot of Transmission as a Function of Wavelength for a 10 mm Thick, Uncoated Sample of UV Fused Silica (Note: Surface Reflections are Included)
| Specifications | |
|---|---|
| Wedge Angle | 5° ± 3 arcmin |
| Size (L x H) | 50.8 mm x 25.4 mm (2.00" x 1.00") |
| Clear Aperture | 45.72 mm x 22.86 mm (1.80" x 0.90") |
| Surface Flatness | λ/4 @ 632 nm (per inch) |
| Surface Quality | 10-5 Scratch-Dig |

Dimensional Drawing of BSF2550 Wedged Plate Beamsplitter
THEORY

Figure 1: Ray tracing and symbol definitions for the wedged beamsplitter.
Determining the Output Angles
By noting that the sum of the angles in a triangle is 180°, it can be shown that:
E1 = A + C,
G1 = 2E1 - C = C + 2A,
where the angles are defined in Figure 1. By continuing to apply these formulas to successive angles, it can be shown that:
GL = C + 2LA,
EL = C + (2L - 1)A
where L is any integer.
In figure 1, each ray output from the system is given a numeric designation; these will be referred to as the “output beam order.” The “even” orders are emitted from one side of the beamsplitter, and the “odd” orders are emitted from the other side, as indicated. Therefore there is a relationship between the beam order m and the angle indexing value L:
For odd values of m: m = 2L - 1
For even values of m: m = 2(L - 1).

Click to Enlarge
Figure 2: The index of refraction vs. wavelength for UV fused silica. Click here for an excel file containing this data.
The angles of refraction for the emerging beams may be calculated using Snell’s law from values of EL and GL. If the small angle approximation is used, then the sine of the angle is approximated by its value in radians, and it can be shown that:
FL = B + (2L - 1)nA
HL = B +2LnA,
where n is the index of refraction. The index of refraction depends on wavelength, a plot for UV Fused Silica is shown in Figure 2.
These expressions can be rewritten as a deviation from the incident beam, D. For the m = -1 beam, the deviation is:
D = 2B.
For the other odd orders, it is:
D = B + H(m+1)/2.
For the even orders, it is:
D = F(m/2)+1 - B - A
=(2m + 1)nA - A.
Remember that these values are approximations, and the real values may vary slightly due to the small angle approximation used in the derivation.
Other Considerations
It is worth noting that there will be a small polarization dependence on the intensity of the transmitted and reflected beams. However, if the angle of incidence is small, then the polarization effects will be minimized. It is also possible to calculate the attenuation experienced by each beam exiting the beamsplitter, the details of this calculation are in the reference.
Reference:
Beers, Y. "The Theory of the Optical Wedge Beam Splitter." NBS Monograph 146 (October 1974).
Part Number | Description | Price | Availability |
|---|---|---|---|
BSF2550 | Customer Inspired! Wedged Plate Beamsplitter, 5° Wedge Angle, 1.0" x 2.0" | $95.63 | 3-5 Days |


